|
© Eric R. Pianka The late Garrett Hardin summarized geometric growth with the simple statement that "what starts off slow, finishes in a flash." Under optimal conditions, the human gut bacterium, Escherichia coli, can double every 20 minutes. Beginning with just a single bacterium, grown in a chemostat at 98.6 degrees F with ample sugar and other food, the population progresses from one to two in the first 20 minutes, then from 2 to 4 in the second 20 minutes, and then from 4 to 8 in the third 20 minutes. So, under ideal conditions, one bacterium becomes 8 in just one hour. If this maximal rate of increase continues for a day and a half, after only 36 hours, a one-foot deep layer of bacteria will cover the entire surface of the Earth (land and oceans). In the next hour, this layer doubles to two feet deep, then four feet deep, and in only 39 hours, the entire planet is covered over with an 8 foot deep layer of bacteria. Such inexorable population growth is known as exponential or geometric growth and leads to J-shaped populaton trajectories through time (see following figure showing bacteria growing exponentially on an agar plate). 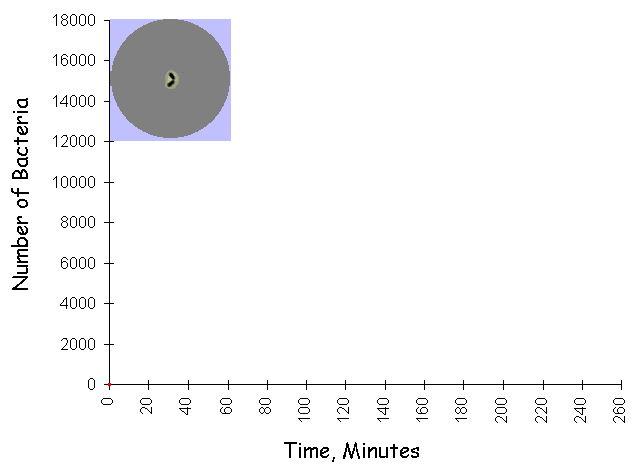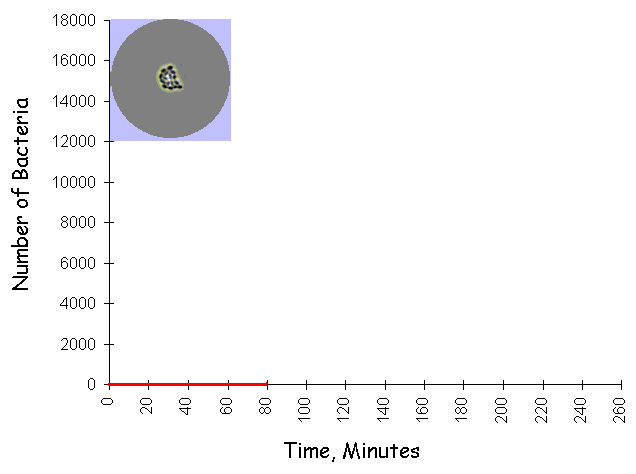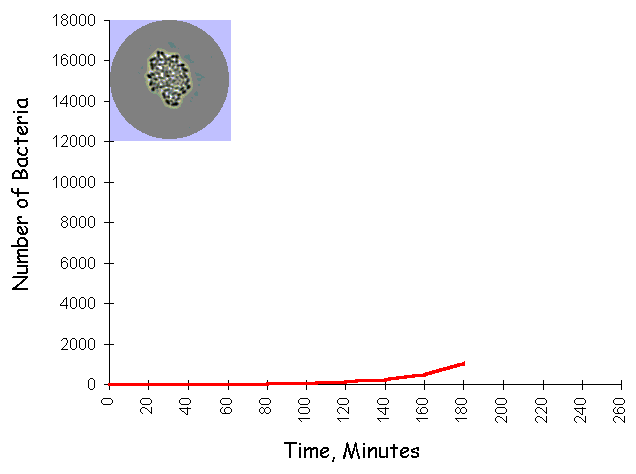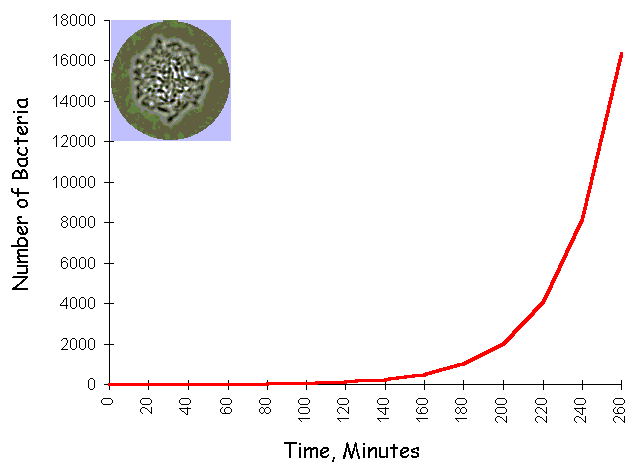 Human populations are growing in exactly the same manner over the land surface of planet Earth. 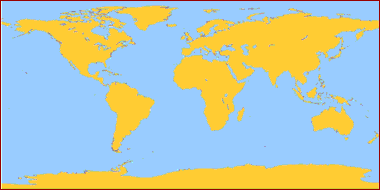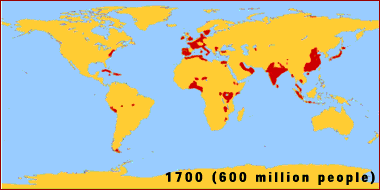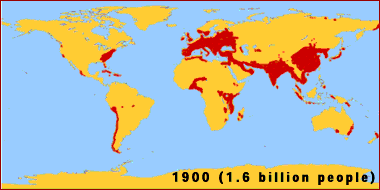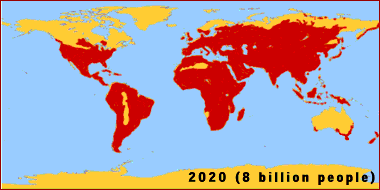
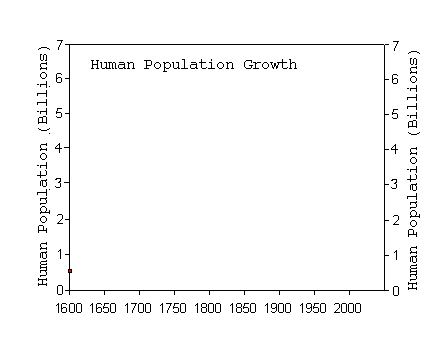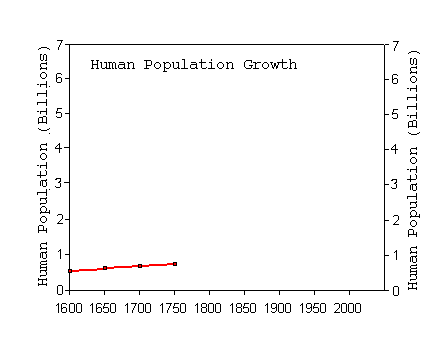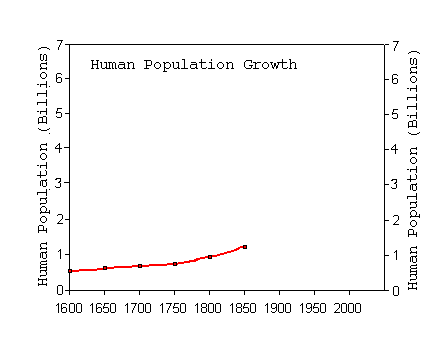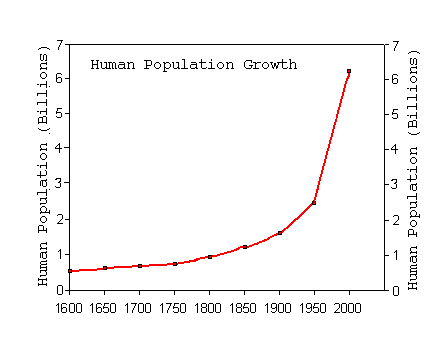
Such runaway population growth cannot be sustained in a finite world and must eventually lead to a population crash, or even extinction, as in the reindeer example shown below. It is just a matter of time until human populations face the same scenario. 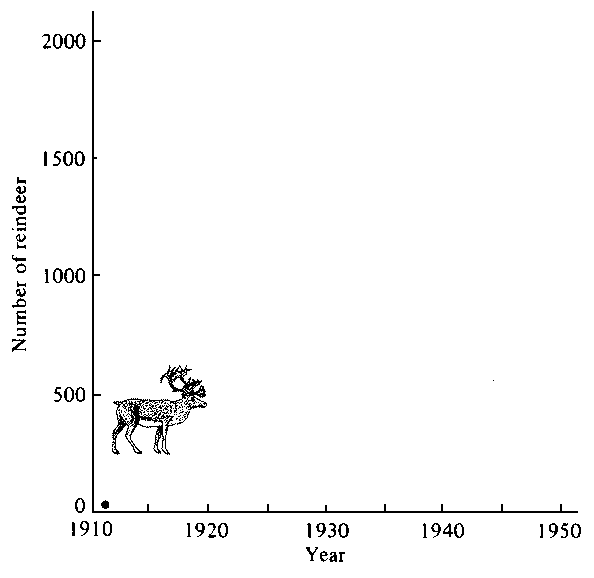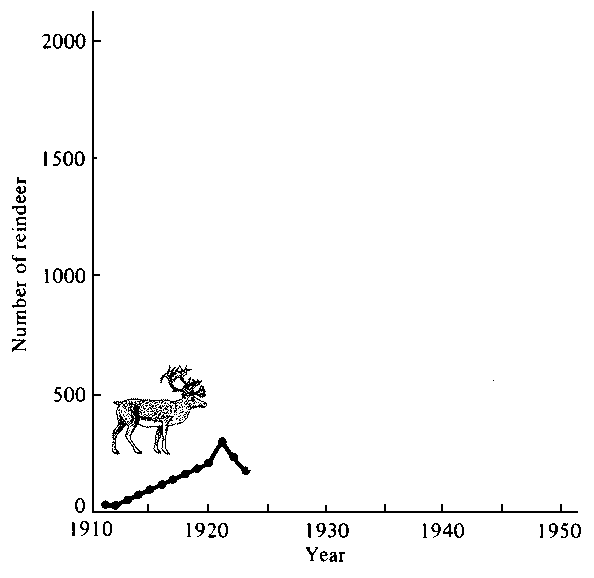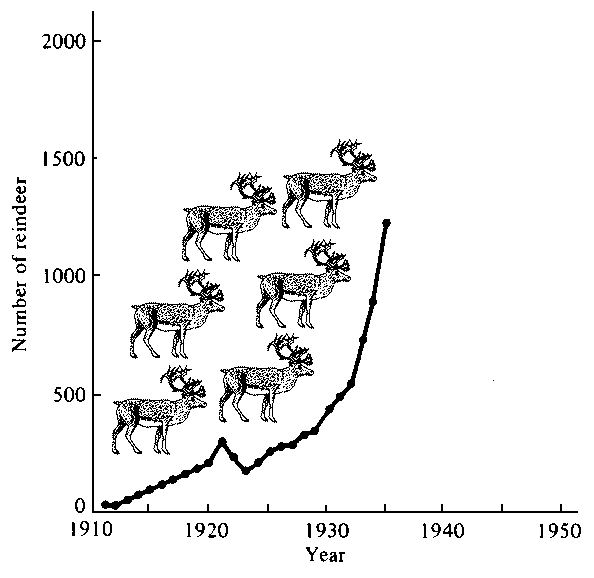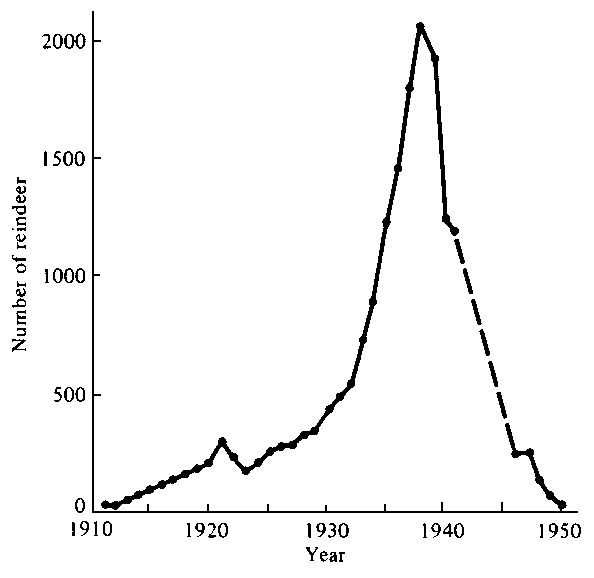 Pianka, E. R. 2000. Evolutionary Ecology, 6th ed. Addison-Wesley. To appreciate how dire the situation is, go to The Clock is Ticking For other perspectives on exponential growth, please watch Exponential Growth Are Humans Smarter than Yeast? Go to Last updated 7 July 2007 by Eric R. Pianka |