17| Community and Ecosystem Ecology
Systems and Macrodescriptors
Except for a brief treatment of biomes, we have until now considered the ecology of individuals and populations. We now consider the highest level of biological organization: entire systems of interacting populations in a complex and dynamic physical environmental setting. This kind of ecology is known as synecology. Synecology is the most abstract and most difficult kind of ecology, but it is also exceedingly tantalizing and vitally important, as well as extremely urgent.
As in any academic endeavor, there are two, almost diametrically opposed, approaches to the ecology of ecosystems: one approach views ecological systems in terms of their component parts, nutrient pools coupled to complex networks of interacting populations. The other approach is more holistic, coming at systems from the top down, rather than from the bottom up. These two perspectives each have their own advantages and limitations, but both have proven to be useful.
Community structure concerns all the various ways in which members of communities relate to and interact with one another, as well as any community-level properties that emerge from these interactions. Just as populations have properties that transcend those of the individuals comprising them, communities seem to have both structure and properties that are not possessed by their component populations. Community ecologists are still in the process of developing a vocabulary. Identification of appropriate aggregate variables or macrodescriptors (Orians 1980a) is essential, but constitutes a double-edged sword; macrodescriptors allow progress but simultaneously constrain direction(s) that can be pursued. To be most useful, macrodescriptors must simplify population-level processes while retaining their essence without fatal oversimplification. Examples include trophic structure, connectance, rates of energy fixation and flow, efficiency, diversity, stability, distributions of relative importance among species, guild structure, successional stages, and so on. At this early stage in community ecology, it seems wise not to become overly "locked in" by words and concepts. Even the trophic level concept should not be inviolate.
Some system-level properties are simply epiphenomena that arise from pooling components; examples would presumably include trophic levels, subwebs, nutrient cycles, and ecological pyramids. But, do communities also possess truly emergent properties that transcend those of mere collections of populations? For example, do patterns of resource utilization among coexisting species become coadjusted so that they mesh together in a meaningful way? If so, truly emergent community-level properties arise as a result of orderly interactions among component populations. This fundamental question needs to be answered. Either way, transcendent phenomena or epiphenomena simply cannot be studied at individual or population levels.
A major problem for community and ecosystem ecologists is that communities are not acted upon directly by natural selection (as individual organisms are). We must keep clearly in mind that natural selection operates by differential reproductive success of individual organisms. It is tempting but dangerously misleading to view organisms or ecosystems as having been "designed" for orderly and efficient function. Antagonistic interactions at the level of individuals and populations (competition, predation, parasitism) must frequently impair certain aspects of ecosystem performance. Effective studies of community organization thus require a pluralism of approaches, including all of the following levels: individuals, family groups, populations, trophic levels, and community networks, as well as historical and biogeographic studies. All these approaches have something useful to offer. The approach taken must be fitted to the questions asked as well as to the peculiarities of the system under study. Much more effort needs to be devoted to connecting community level attributes and phenomena to the behavior and ecology of individual organisms.
Ecosystem-level studies are also plagued by difficult problems of scale in both space and time. Patch size and dynamics, climatic events, nutrient cycles, disturbance frequency, and dispersal ability are just some of the many factors that vary widely within and among systems, as well as over space from local to geographic areas and through time from the short term to the long term.
A plethora of interesting questions can be asked about communities: What structure do they have that transcends population-level processes? What are the effects of community-level attributes on the component organisms living in a given community? What are the roles of parasitism, predation, mutualism, and interspecific competition in shaping community structure? How important are indirect interactions among species and to what extent do such interactions balance out direct effects? How many niche dimensions separate species, and which ones? To what extent are species spread out evenly in niche/resource space? (Such an over-dispersion in niche space might be predicted under a competitive null hypothesis, with each species minimizing its interactions with all others.) Or do clusters of functionally similar species ("guilds") exist? How can such guild structure be detected and measured? What are its components? Are such guilds merely a result of built-in design constraints on consumer species, and/or do guilds simply reflect natural gaps in resource space? Can guild structure evolve even when resources are continuously distributed as a means of reducing diffuse competition? (A community without guild structure would presumably have greater diffuse competition than one with guild structure.) Do more diverse communities have more guild structure than simpler communities? What factors determine the diversity and stability of communities and what is their relationship to one another?
Ultimately, we must be able to answer such fundamental questions about how natural systems are put together before we will even begin to be able to ask more meaningful questions about why ecosystems have any particular observed properties, such as "What are the effects of indirect interactions among populations and/or guild structure on the assembly, structure, stability, and diversity of communities?"
The extreme complexity of most ecosystems makes their study difficult but at the same time quite challenging. The concept of a community is itself an abstraction; communities are seldom clear-cut and distinct but almost always grade into one another. By considering ecological systems as "open" rather than "closed," and by allowing for continual inflow and outflow of materials, energy, and organisms, one can partially overcome this difficulty and the community concept can be quite useful. Thus, communities change both in space and in time, and the picture developed in this chapter is essentially an instantaneous view of a fairly localized portion of a larger community.
Systems Ecology
Ecological communities are exceedingly complex, with a myriad of intricate and often quite subtle interactions between and among their component resources, individuals, and populations. Even a process as fundamental as the interaction between a predator and its prey may require elaborate analysis in terms of numerous subcomponents; these include hunger, search, pursuit and capture, functional and numerical response, escape tactics, spatial and temporal distribution of prey, predator learning and interference between predators, and so on (Holling 1965, 1966). A vigorous branch of ecology termed systems ecology has been developed to deal with such complexity. Systems ecologists exploit computers to build models of complex ecological systems that allow for various sorts of interactions between and among components, which may themselves have many interacting subcomponents. Using actual data on how each component, at each level, affects others (in practice such data are very difficult to obtain), systems ecologists model ecological systems attempting to predict their responses to particular perturbations. Because the systems approach is basically descriptive and deductive, it is limited in that the behavior of a system usually cannot be predicted with accuracy at states outside those used in the original data describing interactions between compartments.
Compartmentation
One obvious way to approach a complex community or ecosystem is to attempt to simplify it by recognizing various more or less "natural" subunits. The extent to which systems can be understood in terms of such arbitrary compartments is not clearly evident. Ultimately, we may have to abandon this sort of approach in favor of a more holistic one.
Trophic Levels
Primary producers, or autotrophs, represent the first trophic level. They are the green plants that use solar energy to produce energy-rich chemicals. Primary producers are an essential part of a community in that practically all other organisms in the community are directly or indirectly dependent on them for energy. Organisms other than the primary producers, or heterotrophs, include consumers and decomposers. Herbivores are primary consumers and represent the second trophic level. Carnivores that eat herbivores are secondary consumers or primary carnivores and are on the third trophic level. Carnivores that eat primary carnivores in turn constitute the fourth trophic level and are termed tertiary consumers or secondary carnivores. Similarly, those that prey on secondary carnivores are quaternary consumers or tertiary carnivores and so on. Because many animals, such as omnivores that eat both plant and animal matter, prey on several different trophic levels simultaneously, it is often impossible to assign them to a given trophic level. Such animals can usually be assigned partial representation in different trophic levels in proportion to the composition of their diet. Another way around this problem is to assign such omnivorous species a position on a trophic continuum (Rigler 1975; Carney et al. 1981; Adams et al. 1983; Cousins 1985). The trophic level concept has proven to be an extremely useful abstract macrodescriptor for the study of community structure; it facilitates examination of the flow of matter and energy through communities and underscores the fundamental differences between interactions that take place within trophic levels (so-called horizontal interactions) as opposed to those that operate between trophic levels (termed vertical interactions).
Major components of an ecosystem can be diagrammed conveniently as shown in Figure 17.1, where each trophic level is treated as a "compartment" and arrows designate the direction of flow of matter and energy. Many materials, including calcium, carbon, nitrogen, and phosphorus, move from compartment to compartment as individual organisms are consumed by others at higher trophic levels, and eventually return to the abiotic "nutrient pool," where they may be reused by primary producers; such movements of matter through ecosystems are termed biogeochemical cycles (see section below). An essential component of any ecosystem is its decomposers, or reducers, which return materials to the nutrient pool. Whereas matter continually circulates through the various compartments of an ecosystem and is always being reused, energy can be used only once. All ecosystems thus depend on a continual inflow of energy.

-
Figure 17.1. A trophic level "compartment" model of a hypothetical community, with arrows indicating the flow of energy through the system. The width of each arrow reflects the rate of flow of energy between particular parts of the system.
Guild Structure
To what extent are species overdispersed in niche/resource space? Do clusters of functionally similar species exist? Root (1967) coined the term guild to describe groups of functionally similar species in a community, such as foliage-gleaning insectivorous birds. In competitive communities, guilds would represent arenas with the potential for intense interspecific competition, with strong interactions within guilds but weaker interactions with the remainder of their community. Techniques for objectively defining a guild remain in their infancy, although the "single-linkage" criterion of cluster analysis allows a guild to be defined ope
nally as follows. A guild is a group of species separated from all other such clusters by an ecological distance greater than the greatest distance between the two most disparate members of the guild concerned. This conservative definition allows complex hierarchical patterns of nesting of smaller guilds within larger ones (Figure 17.2).
-
Figure 17.2. The guild structure of the lizard fauna of the Kalahari semidesert, based on stomach contents (food guilds) and microhabitat usage (microhabitat guilds). Of the 21 species, 12 and 14 are members of a two-species food guild or microhabitat guild, respectively (the opposite member of each pair is the other's nearest neighbor in niche space). All but one (Pachydactylus capensis, a food and microhabitat generalist) of the 21 species is a member of at least one guild. Many two-species guilds are nested inside larger guilds. The microhabitat "superguild" consists of all non-subterranean species, none of which overlap at all with either of the two subterranean species Typhlosaurus lineatus and T. gariepensis. (Note that some species in the same food guild, such as Eremias lineo-ocellata and Meroles suborbitalis, are in different microhabitat guilds.)
Food Webs
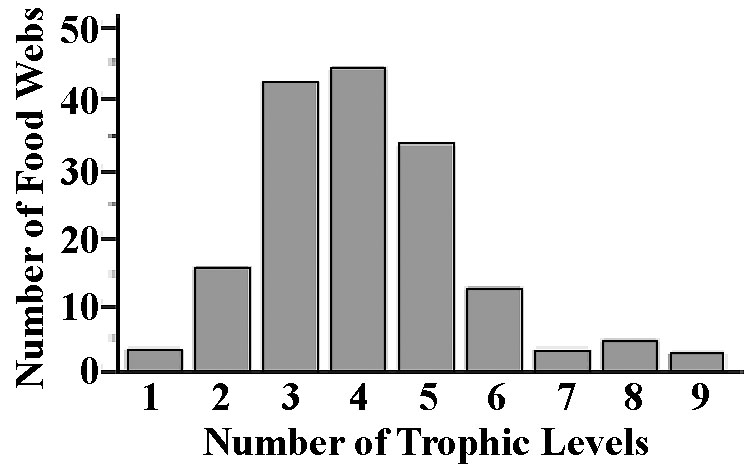
Any community can be represented by a food web, which is simply a diagram of all the trophic relationships among and between its component species. A food web is generally composed of many food chains, each of which represents a single pathway up the food web. Food chains seldom consist of more than five to six links and usually contain only three or four trophic levels (Figure 17.3). A species at the top of a food chain, with no predators of its own, is a top predator. Species at the bottom of food chains are termed basal species. The direction of flow of matter and energy between species is often shown with arrows, as in Figure 17.4. Horizontal interactions within trophic levels are not usually included. Often such food webs depict only whether or not species in different trophic levels interact, but not the actual intensity of this interaction. A really complete food web would also include the rates of flow of energy and materials among the various populations comprising a community. Gathering accurate data on food webs is not easy and the majority of existing data sets are crude and incomplete.
-
Figure 17.3. Histogram of numbers of trophic levels among 183 different food webs.
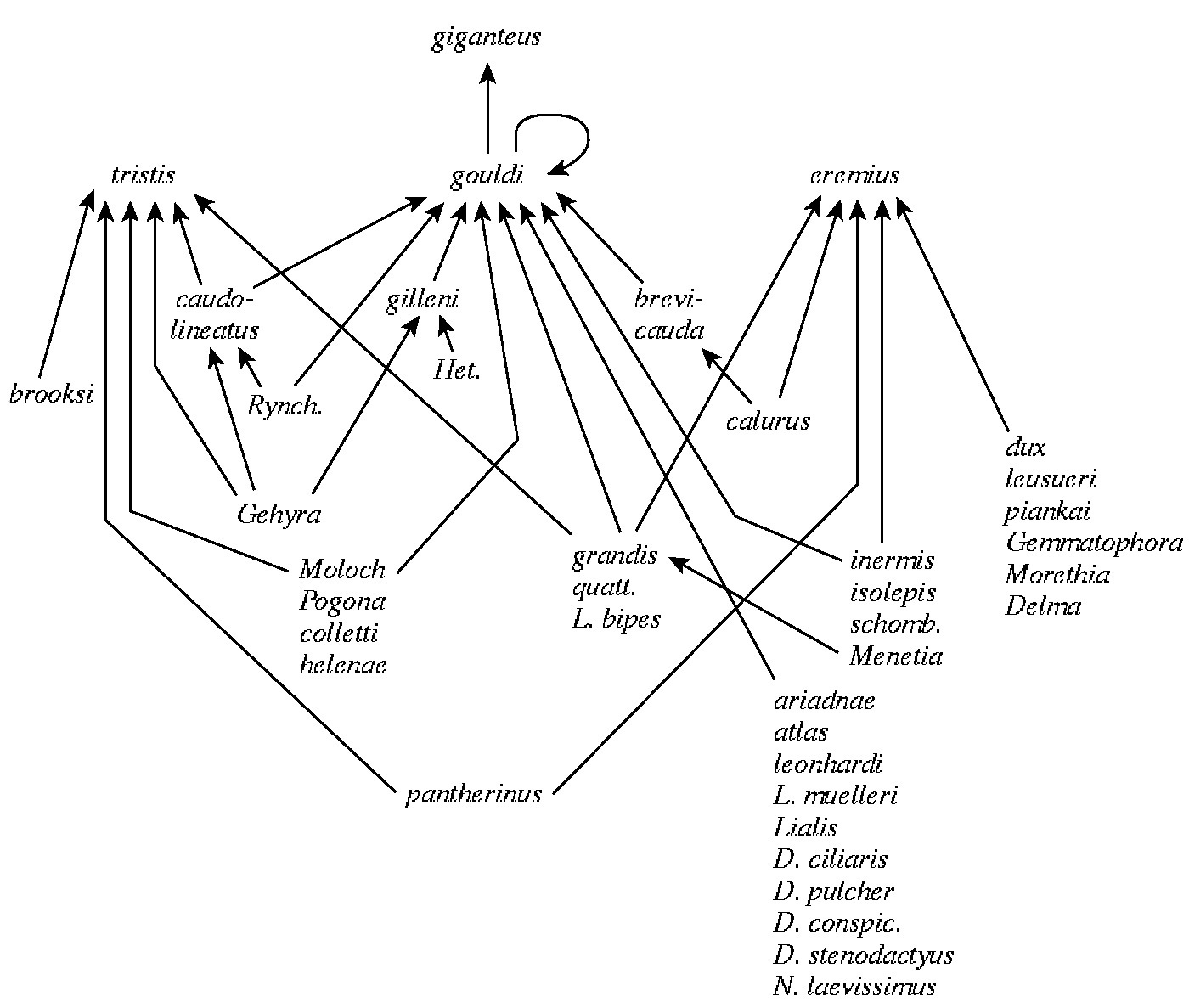
Food webs have recently attracted a lot of interest because they seem to be strongly constrained and exhibit some interesting patterns. A useful concept is the notion of a subweb, or sink food web, which is a portion of an overall food web that ends up being funneled into a particular top predator (Figure 17.4). Such a subweb may constitute a natural ecological unit of study and may serve as a model network of a larger and more complete food web. Food web complexity increases with the number of cross linkages among its component food chains, and this is thought to affect community stability. One means of calculating a simple numerical index of food web complexity is by estimating what is termed connectance, defined as the actual number of connections among members of a food web divided by the total possible number of connections (Pimm 1982). Connectance tends to decrease with increasing numbers of species (more diverse communities have relatively simpler web structures).
-
Figure 17.4. Part of the food web in the Great Victoria Desert of Australia. Each name represents a different lizard species. The "top" predator, a monitor lizard, Varanus giganteus, eats another monitor Varanus gouldii which consumes 27 other species of lizards including 3 species of pygmy monitors. Lizards lower down in the food web feed on various sorts of arthropods, which either prey on other insects or eat plants. A more satisfactory food web would separate all food types into species and would indicate the actual rate of flow of energy up each link, or food chain, in the web.
The Community Matrix
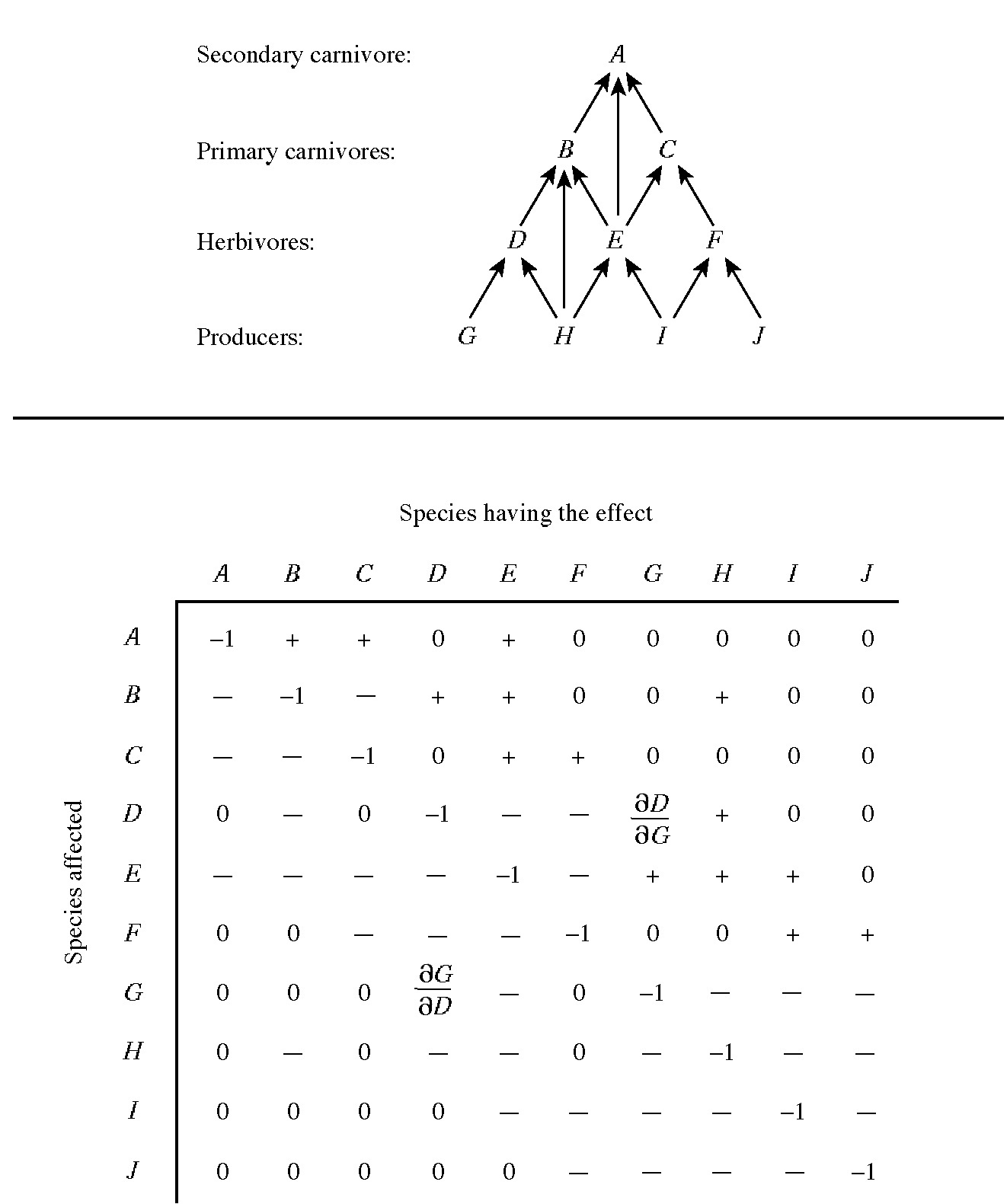
A table of numbers with rows and columns is known as a matrix. Building on the Lotka-Volterra competition equations, Levins (1968) formalized the concept of an alpha matrix, or (more generally) a community matrix. For a community composed of n species, the community matrix is an n x n matrix that gives the sign and degree of interaction between each pair of species. Figure 17.5 illustrates the community matrix of trophic relationships among ten hypothetical species with a food web as shown. In pairs of competing species, values of the partial derivatives are both negative, indicating that each inhibits the other's population. The magnitude of the partial derivative values
-
Figure 17.5. Food web and interaction matrix for a hypothetical ten-species system. Signs of interaction coefficients (partial derivatives that reflect the sensitivity of each species' population density to changes in the density of the others) are given. Only direct interactions between and within two trophic levels are considered. All members of a given trophic level are assumed to be in competition. Higher order interactions, such as the effect of a plant's antiherbivore defenses on a carnivore that depends on the plant's herbivores for food, or the indirect effects of the predator on the plant through reducing herbivore densities, are ignored for simplicity. (A community matrix showing the net effect of each species on every other can also be constructed.) One pair of interaction coefficients is identified within the matrix, that between Species D (predator) and Species G (prey). Note that ∂D/∂G is positive whereas ∂G/∂D is negative. This is a Jacobian matrix. A community matrix can also be formulated using competition coefficients, in which case it is known as an alpha matrix (sign structure is reversed).
indicates the intensity of competitive inhibition, which need not be equal and opposite. A prey-predator or parasite-host relationship is indicated by ∂Ni/∂Nj and ∂Nj/∂Ni values with opposite signs, with the predator or parasite benefiting from the relationship and the prey or host suffering. Again, the degree of benefit or detriment is represented by the magnitude of the interaction coefficients. Thus, if ∂Ni/∂Nj is positive and ∂Nj/∂Ni is negative, species i eats species j. Mutualistic relationships are represented by pairs of positive partial derivatives. Thus the sign structure of such a matrix specifies the trophic structure of a community.
In competitive communities, a greater number of effective niche dimensions will result in fewer off-diagonal elements of zero and more intense diffuse competition ("connectance" increases). Moreover, the guild structure of a community is implicit in its community matrix, since clusters of species that interact strongly will have large coefficients, whereas those that interact weakly will have lower coefficients.
A virtue of the community matrix idea is that it facilitates abstraction and quantification of the interactions among members of a complex community. The concept of the community matrix is actually independent of the Lotka-Volterra equations because it can be formulated equally well in terms of the sensitivities of each species' population density to changes in the densities of other species using partial derivatives. Although one species may affect another in both positive and negative ways simultaneously, the appropriate coefficient in the matrix represents an overall effect. Interaction coefficients in community matrices traditionally represent only the direct pairwise effects of each species on every other; however, indirect effects also occur and may either mitigate or enhance direct interactions. An exactly analogous matrix of net effects, sometimes termed the community effect, between all pairs can also be constructed. Such net community matrices provide useful insights into community structure.
For example, a pair of species that competes in direct pairwise interactions may actually have an overall indirect mutualistic relationship provided that each sufficiently reduces the densities of the other species' other competitors. Indirect mutualisms can also arise in several other ways involving interactions between trophic levels (see Chapter 11). Indirect effects opposite in sign to direct effects can thus reduce or even reverse the overall net effect. Interactions are presumably neither constant nor independent but change both in time and in space and with community composition. Nevertheless, the concept of an ever-changing community matrix is an extremely useful abstraction that helps us begin to visualize and to model what presumably is actually happening in a complex real community.
An emerging idea is that the interactions between any
two populations cannot be understood except within the complex network of other interacting
populations in which the pair concerned is embedded.
Biogeochemical Cycles in Ecosystems
Some chemical elements are much more abundant than others;
for example, iron, oxygen, and silicon are very common, whereas potassium, calcium, and phosphorus
are relatively uncommon, at least on the surface of the planet Earth. Organisms expend energy to
concentrate and retain certain rare elements in their tissues. A relatively few ions are vitally
important to carbon-based living systems, particularly calcium, sodium, potassium, nitrate,
phosphate, sulfate, and carbonate. Different nutrients are recycled through ecosystems and
nutrient pools at different rates and in different ways. Numerous such cycles exist; among the
most important are those involving oxygen, carbon, sodium, calcium, nitrogen, sulfur, and, of
course, water. These movements of materials through organisms and various ecosystems are very
complex but quite interesting and important. Figure 17.6 depicts one such cycle, that of calcium,
which circulates in a wide variety of
-
Figure 17.6. A biogeochemical cycle: major movements of calcium are
represented diagrammatically. Many other materials circulate within and between ecosystems in
somewhat similar fashions. [From Whittaker (1970). Communities and Ecosystems. Reprinted with
permission of Macmillan Publishing Company, Inc. Copyright © 1970 by Robert H. Whittaker.]
different ways at very different rates in and between various biotic and abiotic components. Biogeochemical cycles markedly affect the physical environments experienced by organisms. If a biogeochemical cycle is closed, nutrients are returned to a nutrient pool and tightly recycled within a system. However, many nutrient cycles are not closed but exhibit losses from the system concerned to other systems. Whereas most gaseous cycles, such as those in the atmosphere, are closed, aqueous and sedimentary cycles are frequently not closed. Rates of turnover of nutrients in various biogeochemical cycles, as well as available reservoirs, determine "residence times" and are of substantial interest in ecosystem ecology because they profoundly affect a system's productivity as well as its resilience. Slow turnover rates reduce stability and productivity, whereas rapid rates of nutrient cycling confer stability on ecosystems and enhance productivity.
Because human activities, especially burning of fossil fuels, have markedly increased the concentration of the greenhouse gas carbon dioxide in the atmosphere, which in turn has resulted in global warming, the carbon cycle is of great current interest.
The oceans constitute a major reservoir for many materials -- rivers carry an unceasing supply of dissolved solutes, as well as various suspended materials, the most important of which are soils (silts). Much of this inexorable flow is essentially one way, but on a geological time scale, even seafloors are eventually destined to become landmasses. Virtually all materials must make this inevitable journey to the sea. Rainwater dissolves certain rocks, particularly limestones (calcium carbonate); it also leaches all sorts of water-soluble nutrients out of soils. A steady supply of materials such as calcium, potassium, sodium, carbonate, nitrate, and phosphate thus flows steadily into the seas. Except for sodium and chloride, almost all of these ions are removed from seawater either by organisms or by precipitation to wind up on the seafloor in ocean sediments, either as dead organisms or precipitates. Once there, materials remain locked up and out of commission for millennia. Thus, this huge reservoir displays a very long average residence time. Oceanic chemistry is also maintained by a geochemical cycle; its salt concentration, or salinity, of about 35 parts per thousand NaCl, represents an equilibrium, which has probably persisted since before life began.
Principles of Thermodynamics
An important facet of community ecology is the energy relationships between and among members of a community. Before studying community energetics, however, we must briefly review some fundamentals of thermodynamics.
All organisms require energy to persist and to replace themselves, and the ultimate source of practically all the earth's energy is the sun. One can think of the sun as "feeding" the earth via its radiant energy. But 99 percent or more of this incident solar radiation goes unused by organisms and is lost as heat and heat of evaporation; only about 1 percent is actually captured by plants in photosynthesis and stored as chemical energy. Moreover, energy available from sunlight varies widely over the earth's surface both in space and in time (see Chapter 3).
Physics and chemistry have produced two basic laws of thermodynamics that are obeyed by all forms of matter and energy, including living organisms. The first law is that of "conservation of matter and energy," which states that matter and energy cannot be created or destroyed. Matter and energy can be transformed, and energy can be converted from one form into another, but the total of the equivalent amounts of both must always remain constant. Light can be changed into heat, kinetic energy, and/or potential energy. Whenever energy is converted from one form into another, some of it is given off as heat, which is the most random form of energy. Indeed, the only energy conversion that is 100 percent efficient is conversion to heat, or burning. Burning aliquots of dried organisms in "bomb calorimeters" is a common method of determining how much energy is stored in their tissues (Paine 1971). Energy can be measured in a variety of different units such as ergs and joules, but the common denominator used in ecology is heat energy or calories.
The second law of thermodynamics states that energy of all sorts, whether it be light, potential, chemical, kinetic, or whatever, tends to change itself spontaneously into a more random, or less organized, form. This law is sometimes stated as "entropy increases" -- entropy being random, unavailable energy. Suppose I heat a skillet to cook an egg, and after finishing I leave it on the stove. At first, heat energy is concentrated near the skillet, which is, relative to the rest of the room, quite nonrandom. But by the next morning the skillet has cooled to air temperature, and the heat energy has radiated throughout the room. That heat energy is now dispersed and unavailable for cooking; the system of the skillet, the room, and the heat has gone toward equilibrium, become more random, and entropy has increased. Unless an outside source of energy such as a stove, with fuel or electricity, is continually at work to maintain a nonequilibrium state, dispersion of heat results in a random equilibrium state. The same is true for all kinds of energy. According to this law, our solar system and presumably the entire universe should theoretically become a completely random array of molecules and heat in the far distant future.
Life has sometimes been called "reverse entropy" (negentropy) because organisms maintain complex organized states compared to their surroundings. But they obey the second law just as any other system of matter and energy; all organisms must work continually to build and maintain nonrandom assemblages of matter and energy. This process requires energy, and organisms use the energy of the decaying sun (which, of course, also obeys the second law of thermodynamics and tends toward increasing disorder) to "oppose" the second law within their own tissues by producing order out of increasing disorderliness. Wherever there is a live plant or animal, there must be an energy source. Without a continued influx of energy, no organism can survive for very long. Again, this "reverse entropy" occurs only within each organism, and the overall energy relations of the entire solar system are in accord with the second law of thermodynamics, with the overall system continually becoming more and more random.
Pyramids of Energy, Numbers, and Biomass
The rate of flow of energy through a given trophic level decreases with increasing trophic level for several reasons. Because energy transfers are never 100 percent efficient, not all the energy contained in any given prey item is actually available to a predator; some is lost in converting prey tissue into predator tissue, and some is not even assimilated but passes through the predator's intestinal tract unchanged and is then decomposed by reducers. The efficiency of transfer of matter and energy from prey to predator is often greatly reduced by predator-avoidance tactics of prey, such as the chemical defenses of plants. In addition, each organismic unit (and each trophic level) expends some of its available energy on its own activities, further reducing the amount of energy available at higher trophic levels. Ultimately, of course, at equilibrium all the energy captured by primary producers must be expended and dissipated back into space as heat; that is, the amount of energy entering the system must exactly balance that leaving it.
The reduction in the rate of flow of energy from each trophic level to the next higher one determines many of a community's properties, including the total number of trophic levels as well as the proportion of predators to prey. Ecologists estimate that after standardization per unit area and unit time, approximately 10 to 20 percent of the energy at any given trophic level is available to the next higher trophic level. Hence, if a thousand calories are available to primary producers, usually only a few of the thousand are actually available to a secondary carnivore three trophic levels away. A result of this rapid reduction in the availability of energy is that animals at higher trophic levels are generally much rarer than those at lower ones. Moreover, decreasing availability of energy places a distinct upper limit on the number of trophic levels possible, with about five or six being the normal maximum.
A convenient means of expressing the energetic structure of a community is the pyramid of energy, which consists simply of the rates of energy flow between various trophic levels (Figure 17.7). The laws of thermodynamics and the preceding considerations dictate that the pyramid of energy can never be inverted; that is, the flow of energy through each trophic level must always decrease with increasing trophic level.
Two other types of ecological "pyramids" are the pyramid of numbers and the pyramid of biomass. These are instantaneous measures rather than rates; they have no time dimension (units of the pyramid of energy are calories per square meter per year, but
-
Figure 17.7. Pyramid of energy for Silver Springs, Florida. P = plants, H = herbivores, C = carnivores, TC = top carnivores. [From Phillipson (1966) after Odum.]
the units of the pyramid of numbers are numbers per square meter, and the units of the pyramid of biomass are grams per square meter). The pyramid of numbers consists of a set of the densities of individuals in each trophic level; the pyramid of biomass is the biomass (usually measured in grams dry weight) per square or cubic meter in each trophic level. Pyramids of numbers and biomass measure only the standing crop (the amount present at an instant) of each trophic level, not their turnover rate. Because they lack a time dimension, these two pyramids may be inverted, with, for example, lower densities and/or smaller biomasses at lower trophic levels. Thus, one tree may support many insects (an inverted pyramid of numbers); likewise, a rapid rate of turnover allows a small biomass of prey to support a larger biomass of predators with a slower turnover rate. Such an inverted pyramid of biomass often characterizes aquatic ecosystems, where primary producers (phytoplanktonic algae) are small and rapidly dividing, whereas their zooplanktonic predators are larger and longer lived (Figure 17.8).
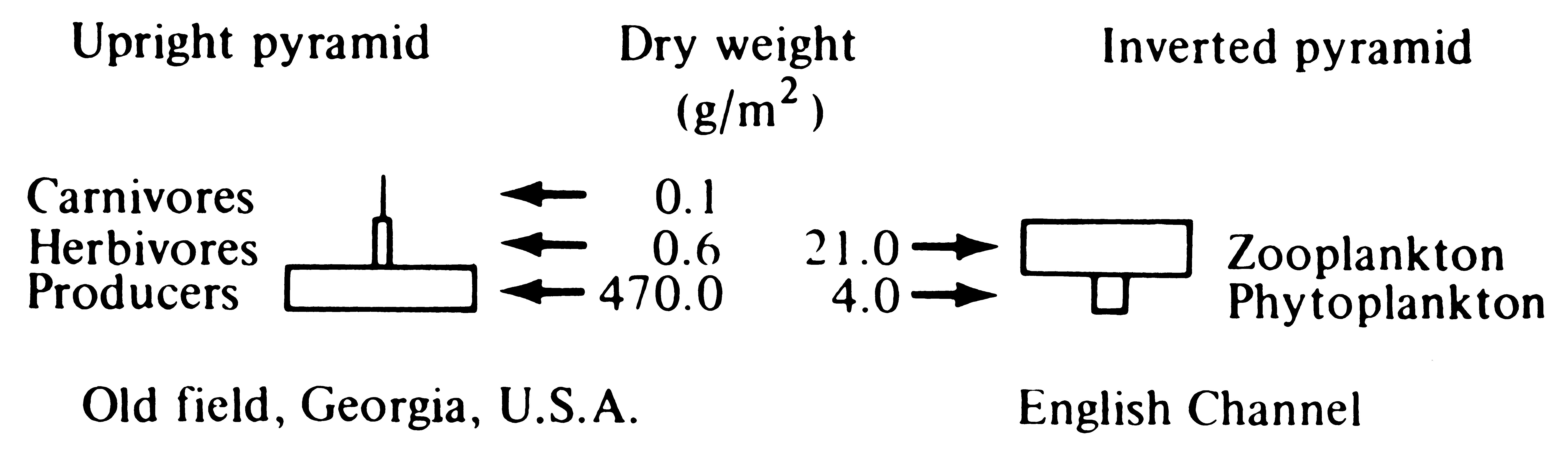
-
Figure 17.8. Two pyramids of biomass, one upright and one inverted. [From Phillipson (1966) after Odum.]
Energy Flow and Ecological Energetics
The energy content of a trophic level at any instant (i.e., its standing crop in energy) is usually represented by capital lambda, Λ, with a subscript to indicate the appropriate trophic level: Λ1 = primary producers, Λ2 = herbivores, Λ3 = primary carnivores, and so on. Similarly, the rate of flow of energy between trophic levels is designated by lower case lambdas, λij , where the i and j subscripts indicate the two trophic levels involved, with i representing the level receiving and j the level losing energy. Subscripts of zero denote the world external to the system; subscripts of 1, 2, 3, and so on, indicate trophic level as previously stated.
-
Figure 17.9. Another compartment model of an ecosystem. Energy flow is shown with solid arrows and the flow of matter with dashed arrows.
Using these conventions, one can represent an ecosystem by a compartment model, as in Figure 17.9. At equilibrium, the amount of energy contained in every compartment (trophic level) must be constant, which in turn requires that the rate of flow of energy into each compartment be exactly balanced by the flow of energy out of the compartment concerned. At equilibrium (dΛi/dt = 0 for all i), energy flow in the system portrayed in the figure may thus be represented by a set of simple equations (with inputs on the left and rate of outflow to the right of the equal signs):
 λ10 = λ01 + λ02 + λ03 + λ04 λ10 = λ01 + λ02 + λ03 + λ04
 λ10 = λ21 + λ01 + λ41 λ10 = λ21 + λ01 + λ41
 λ21 = λ32 + λ02 + λ42 λ21 = λ32 + λ02 + λ42
 λ32 = λ03 + λ43 λ32 = λ03 + λ43
 λ41 + λ42 + λ43 = λ04 λ41 + λ42 + λ43 = λ04
The rate at which energy is actually captured by plants (λ10) is estimated at only about 1 percent of the total solar energy hitting the earth's surface. This rate of uptake of solar energy by primary producers, λ10, is termed the gross productivity. It is usually given in calories/m2/year, which represents the gross annual production (GAP) . Because plants use some of this energy in their own respiration (i.e., (λ01), only a part of the gross annual production is actually available to animals and decomposers; this fraction, λ21, plus the energy used by decomposers, λ41, is termed the net productivity or (on an annual areal basis) net annual production (NAP). Net production may be considerably less than gross production; in some tropical rain forests, plants use as much as 75 to 80 percent of their gross production in respiration. In temperate deciduous forests, respiration is usually 50 to 75 percent of gross primary production, whereas in most other communities, it is about 25 to 50 percent of gross production.
Only about 5 to 10 percent of plant food on land is actually harvested by animals; the remainder of the net primary production is consumed by decomposers. Efficiency of transfer of energy from one trophic level to the next higher trophic level, say, level i to level j, may be estimated as λji / λih, where j = i + 1 and h = i - 1. Thus, the ratio λ21/ λ10 measures the efficiency with which primary producers pass solar energy they capture on to herbivores and, indirectly, to consumers at higher trophic levels. Such ecological efficiencies of transfer of energy from one trophic level to the next are generally estimated to be between about 5 and 30 percent, and a reasonable average figure is about 10 to 15 percent (Slobodkin 1960, 1962). Natural selection operating on individual prey organisms favors escape ability, which in turn reduces the rate of flow of matter and energy through that trophic level, decreasing ecological efficiency but increasing community stability. In contrast, predators evolve so as to be better able to capture their prey, which increases the efficiency of flow of energy through trophic levels but reduces a system's stability. In the coevolution of a predator and its prey, to avoid extinction, the prey must remain a step ahead of its predator. As a corollary, community-level properties of ecological efficiency and community stability may in fact be inversely related because natural selection operates at the level of individual predators and prey. Moreover, the apparent constancy and low level (10 to 15 percent) of ecological efficiency could be a result of the "compromise" that must be reached between prey and their predators. Human efforts to raise ecological efficiencies (monocultures in agriculture and the "green revolution") may be doomed to lead to unstable artifical ecosystems.
Energy flow diagrams have been constructed for some natural communities (Figures 17.10 and 17.11); these diagrams underscore the relatively minor energetic importance of carnivores in ecological systems. Decomposers often play a major energetic role, especially in terrestrial ecosystems where much of the primary production is not consumed by herbivores but instead falls to the ground as dead leaves and other plant material. Indeed, as much as 90 percent of the net annual production in some communities may be consumed by their decomposers. Community ecologists are currently investigating energy flow and efficiency of transfer of energy in natural ecosystems, and much remains to be learned about ecological energetics; such studies have obvious practical significance to human exploitation of ecological systems.
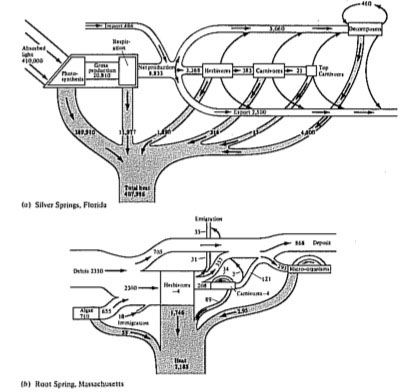
-
Figure 17.10. Two energy flow diagrams from actual communities. Figures are in kcal/m2/year; numbers in boxes in (b) represent changes in standing crops. [From Phillipson (1966) after Teal and Odum.]
-
Figure 17.11. Energy flow diagrams for two ecosystems with very different standing crops. (a) A marine bay. (b) A forest. Standing crop biomass measured in kcal/m2; energy flow in kcal/m2/day. [From Phillipson (1966) after Odum, Connell, and Davenport.]
Secondary Succession
In the southeastern United States, an abandoned field allowed to change naturally is in turn invaded by annual weeds such as crabgrass and asters, then by broomsedge and small perennials, various shrubby species of perennials, pine trees, and finally by oak and hickory trees (Figure 17.12). The composition of the avifauna and bird species diversity also change drastically with these successional changes in the vegetation and are part of the community succession. Plants in each stage modify the environment, presumably making it more suitable for other species in following stages. Typically, shade tolerance and competitive ability increase as succession proceeds. The entire process of secondary succession may take many years (over a hundred years in the preceding example). Only the oak-hickory forest is a stable community in a dynamic equilibrium that replaces itself; such a final stage in succession is termed its climax. In deserts, where the open vegetation alters microclimates very little and soil formation is virtually nonexistent, the first plants to invade are usually the climax species, and the succession, if one calls it such, is short. Earth's biomes (Chapter 4) represent the climax communities that prevail at different localities. Disturbances, both human made and natural (lightning, fires, droughts, landslides, hurricanes, floods), are often frequent enough that extensive areas have not had time enough to reach their own climax state. An equilibrium is reached whereby the proportion of a habitat supporting early successional stages is determined by the frequency of disturbance. Largely undisturbed areas may be primarily in the climax state. During the course of succession, annual production exceeds annual respiration, and organic materials accumulate to form soils and, generally, an increasingly larger biomass of plants and animals. At climax, production equals respiration and organic materials cease to accumulate.
-
Figure 17.12. The typical pattern of secondary succession of vegetation and the avifauna on abandoned farmland in the southeastern United States. Number of bird species increases markedly with increased vertical structural complexity of the vegetation. [From MacArthur and Connell (1966) after Odum.]
Terrestrial succession offers a possible example of how community-level properties could emerge from those of individuals. A fast rate of photosynthesis and hence a rapid growth rate are presumably incompatible with shade tolerance, and hence competitive ability in a light-limited situation. In contrast, shade tolerance and an ability to compete require slower rates of photosynthesis and growth. Such physiological trade-offs at the level of individuals could very well dictate many of the sequential patterns of species replacement (i.e., colonizing species to climax species) that characterize terrestrial succession. More thought needs to be devoted to such attempts to connect community properties with those of individuals in populations.
An illuminating analysis of secondary succession was carried out by Horn (1975b) for forests in the northeastern United States. Horn viewed these forests as honeycombs of independent "cells," each occupied by a particular tree. Percentages of saplings of different species observed under various species of canopy trees were used to construct
a type of projection matrix known as a transition matrix (Table 17.1). This matrix allowed estimation of a probability transition matrix, whose elements contain probabilities that a cell currently occupied by a particular species will be occupied by the same or an alternative species at the next time step. By definition, columns of this matrix sum to 1, and the leading eigenvalue is equal to 1. Multiplying the vector containing relative measures of abundance of each species by this probability transition matrix models the dynamics of community species composition in a manner exactly equivalent to the way in which Leslie matrices model age-structured populations (Chapter 8). The eigenvector associated with the leading eigenvalue of the probability transition matrix indicates the "stable state (or species) distribution" of relative abundances of species (for exactly the same reasons as the stable age distribution is an eigenvector of the Leslie matrix). Used to predict the species composition of a "climax forest," it compares reasonably well to the species composition actually observed in a 350-year-old forest (compare the last two lines of Table 17.2).
Table 17.1 Transition Matrix for Institute Woods in Princeton
_______________________________________________________________________________
Canopy Sapling Species (%) Sapling Species (%)
Species BTA BTA GB GB SF SF BG BG SG SG WO WO OK OK HI HI TU TU RM RM BE BE Total Total
________________________________________________________________________________
BT Aspen 3 3 5 5 9 9 6 6 6 6 - - 2 2 4 4 2 2 60 60 3 3 104 104
Gray birch - - - - 47 47 12 12 8 8 2 2 8 8 0 0 3 3 17 17 3 3 837 837
Sassafras 3 3 1 1 10 10 3 3 6 6 3 3 10 10 12 12 - - 37 37 15 15 68 68
Blackgum 1 1 1 1 3 3 20 20 9 9 1 1 7 7 6 6 10 10 25 25 17 17 80 80
Sweetgum - - - - 16 16 0 0 31 31 0 0 7 7 7 7 5 5 27 27 7 7 662 662
White Oak - - - - 6 6 7 7 4 4 10 10 7 7 3 3 14 14 32 32 17 17 71 71
Red Oak - - - - 2 2 11 11 7 7 6 6 8 8 8 8 8 8 33 33 17 17 266 266
Hickory - - - - 1 1 3 3 1 1 3 3 13 13 4 4 9 9 49 49 17 17 223 223
Tuliptree - - - - 2 2 4 4 4 4 - - 11 11 7 7 9 9 29 29 34 34 81 81
Red Maple - - - - 13 13 10 10 9 9 2 2 8 8 19 19 3 3 13 13 23 23 489 489
Beech - - - - - - 2 2 1 1 1 1  1 1 1 1 8 8 6 6 80 80 405 405
_________________________________________________________________________________
Note: The number of saplings of each species listed in the row at the top, where abbreviations are
self-explanatory, is expressed as a percentage of the total number of saplings (last column) found under canopy individuals of
the species listed in the first column. Entries are percentages of individuals of species listed on the left that will be replaced
one generation hence by species listed at the top. Percentages of "self-replacements" shown in boldface. Total number of
saplings is 3286. A dash indicates that no saplings of that species were found beneath the canopy; a zero, that the percentage was
less than 0.5 percent. The number of big tooth aspen trees in the next generation is BTA(next) = 0.03 BTA + 0.03 SF + 0.01 BG,
likewise, the number of gray birch in the next generation is GB(next) = 0.05 BTA + 0.01 SF + 0.01 BG. Source: From Horn (1975b).
Table 17.2 Distributions of Trees Observed in 4 Forests and Predicted Climax
______________________________________________________________________________
Age (years) BTA BTA GB GB SF SF BG BG SG SG WO WO OK OK HI HI TU TU RM RM BE BE
______________________________________________________________________________
 25 25 0 0 49 49 2 2 7 7 18 18 0 0 3 3 0 0 0 0 20 20 1 1
 65 65 26 26 6 6 0 0 45 45 0 0 0 0 12 12 1 1 4 4 6 6 0 0
 150 150 - - - - 0 0 1 1 5 5 0 0 22 22 0 0 0 0 70 70 2 2
 350 350 - - - - - - 6 6 - - 3 3 - - 0 0 14 14 1 1 76 76
Predicted
climax  0 0 0 0 2 2 3 3 4 4 2 2 4 4 6 6 6 6 10 10 63 63
______________________________________________________________________________
Source: From Horn (1975b).
Evolutionary Convergence and Ecological Equivalence
Organisms evolving independently of one another under similar
environmental conditions have sometimes responded to similar selective pressures with nearly identical
adaptations. Thus, flightless birds such as the emu, ostrich, and rhea fill very similar ecological niches
on different continents. Arid regions of South Africa support a wide variety of euphorbeaceous plants,
some of which are strikingly close to American cacti phenotypically. A bird of some African prairies and
grasslands, the African yellow-throated longclaw (Macronix croceus), looks and acts so much like
an American meadowlark (Sturnella magna) that a competent bird watcher might mistake them for
the same species; and yet they belong to different avian families (Figure 17.13f). Such convergent
phenotypic responses by different stocks of plants or animals are known as
evolutionary convergence.
Products of convergent evolution, organisms that have evolved independently and yet occupy roughly similar niches in various communities in different parts of the world, are known as ecological equivalents. More striking examples of evolutionary convergence (Figure 17.13) usually fall into either or both of two categories. They sometimes occur in relatively simple communities in which biotic interactions are highly predictable and the resulting number of different ways of exploiting the environment are few, and/or they occur under unusual conditions where selective forces for achievement of a particular mode of existence are particularly strong. Examples of the latter include the independently evolved marsupial and placental "saber-toothed tigers" (Figure 17.13e) and the fusiform shapes of sharks, ichthyosaurs, and dolphins. Evolutionary convergence can easily be read into a situation by placing undue emphasis upon superficial similarities but failing to appreciate fully the inevitable dissimilarities between pairs of supposed ecological equivalents.
Often roughly similar ecological systems support relatively few conspicuous ecological equivalents but instead are composed largely of distinctly different plant and animal types. For instance, although the bird species diversities of temperate forests in eastern North America and eastern Australia are similar (Recher 1969), many avian niches appear to be fundamentally different on the two continents. Honeyeaters and parrots are conspicuous in Australia whereas hummingbirds and woodpeckers are entirely absent. Apparently different combinations of the various avian ecological activities are possible; thus, an Australian honeyeater might combine aspects of the food and place niches exploited in North America by both warblers and hummingbirds. An analogy can be made by comparing the "total avian niche space" to a deck of cards. There are a limited number of ways in which this niche space can be exploited, and each bird population or species has its own ways of doing things, or its own "hand of cards," determined in part by what other species in the community are doing.

-
Figure 17.13. Examples of convergent evolution in animals. Pairs of independently evolved but ecologically similar species that occupy similar niches in different communities are known as "ecological equivalents." (a) An Australian agamid lizard, Ctenophorus cristatus (left) and a North American iguanid, Callisaurus draconoides. (b) The Australian thorny devil Moloch horridus (above) and an American desert horned lizard Phrynosoma platyrhinos (below) (c) An African civet (left) and an American weasel. (d) An Australian marsupial, a wombat (left) with its skull and an American placental, a woodchuck, with its skull. (e) Skulls of two fossil (but not contemporary) saber-tooth carnivores, the South American marsupial "cat," Thylacosmilus (left), and the North and South American placental saber-toothed tiger, Smilodon. (f) An American icterid, the eastern meadowlark, Sturnella neglecta (above), and an African motacillid, the yellow-throated longclaw, Macronix croceus. (g) A North American little auk (above) and a Magellan diving petrel, which belong to two different avian orders. [c, d, e after Salthe (1972), Evolutionary Biology. Copyright © 1972 by Holt, Rinehart and Winston, Inc. Reprinted by permission of Holt, Rinehart and Winston, Inc. a, b after Pianka (1971a, 1986a). f, g after Fisher and Peterson (1964).]
Community Evolution
Many communities change during the lifetimes of the individuals that comprise them. In addition to relatively short-term changes during ecological time, community characteristics are affected by evolution of and coevolution among the species' populations that are available to form the community over evolutionary time. At the same time, the community itself is a major determinant of the selective milieu of its component populations, and its characteristics presumably dictate many of their adaptations. The so-called taxon cycle (Chapter 19) is thought to be driven by biotic responses to competition and predation, or "counteradaptations" of the other species in a community (Ricklefs and Cox 1972). Competition within, between, and among species results in the evolution of niche differences, which in turn ensures that the resources of a given community, including plants and animals, are utilized more or less in proportion to their effective supply.
As pointed out earlier in this chapter, evolution of the species within a community has still other effects upon community structure. Evolution of prey reduces the efficiency of transfer of energy from one trophic level to the next but increases stability, whereas evolution of predators acts to increase the efficiency of this transfer but reduces stability. The diversity of prey eaten by a predator as well as the predator's ability to alter its diet with changes in prey availability probably influences the stability of prey populations, and therefore of the community.
Can natural selection operate between entire communities? The notions of selection at the levels of communities and ecosystems (Dunbar 1960, 1968; Lewontin 1970) constitute apparent extremes of the idea of group selection. Unstable systems would seem to be less likely to persist than stable ones; however, selection is unlikely to occur at these levels, in view of both the limited number of communities and ecosystems and their extremely low rate of turnover. Most important, selection acts only by differential reproduction, and it is most difficult to envision reproduction by a community or an ecosystem. Organisms comprising a community are not bound together by obligate relations; instead each evolves in a manner independent of, and often antagonistic to, other members of the community, such as its prey, competitors, and predators. Indeed, as discussed above, community stability may even be incompatible with efficient transfer of energy to higher trophic levels because of the antagonistic interactions between predators and their prey.
Pseudocommunities
Communities are so complex that it is exceedingly difficult to study them even when relatively little is known. The situation is greatly exacerbated when a lot is known -- quite simply, communities are unmanageably complicated. Not only is it all but impossible to collect adequate data on such complex systems, but also comparisons between networks are fraught with almost insurmountable difficulties.
Manipulative experiments, even if feasible, are of limited utility due to indirect effects in complex networks. A promising technique for beginning to tease apart complex systems involves construction of various sorts of "pseudocommunities" based on real prototypes, and against which they can be compared. It is no simple matter to construct random pseudocommunities from real ones: inevitably some of the structure of the prototype is mirrored in the randomized replicate [Colwell and Winkler (1984) term this the "Narcissus effect"]. Such randomly constructed null models of various kinds differ from real systems in interesting ways: similarity among consumers is typically higher and more homogeneous and guild structure is less than in real systems. Pseudocommunities provide useful insight into the distinction between epiphenomena versus truly emergent community-level properties: to the extent that patterns of resource utilization among coexisting members of a community are "coadjusted" so that they mesh together in a meaningful way, a system has emergent properties. The degree to which consumers actually utilize resources disproportionately to their supply can be quantified with utilizations or "electivities" (Ivlev 1961; Pianka 1986a; Winemiller and Pianka 1990).
An assemblage of consumer species can be viewed as being somewhat analogous to a gearbox, with the electivities of various species representing the "cogs" meshing more or less neatly together. Real assemblages can be compared with "pseudo-communities" in an attempt to ascertain just how good such fits among sympatric consumers actually are.
How well do resource utilization patterns observed among sympatric species in a given system "fit" together? Can evidence be found for ecological adjustments among coexisting species? To address these questions, I undertook a fairly extensive series of artificial "removal-introduction experiments" using data on lizard abundances and diets (Pianka 1986a). Resource matrices for diets were assembled and analyzed to estimate the "electivities" of each consumer species on each prey resource state over many different study sites. Each "resident" lizard species on every study site was then systematically replaced by the same species as it was actually observed on each of the other study areas where that species occurred naturally (these are termed "aliens"). A moderately large number of such "transplants" can be made -- for a ubiquitous species found on ten study areas, nine alien "introductions" are possible on each site, allowing a total of 90 alien versus resident comparisons. Resource utilization spectra of all other resident species are left exactly as observed. As one possible measure of the "goodness of fit" among species, assume that the system is approximated by the Lotka-Volterra competition equations. (Consumer species are thus assumed to have reached dynamic equilibria with one another and observed relative abundances are proportional to equilibrium abundances. Moreover, observed dietary similarities are assumed to approximate competition coefficients.)
The diffuse competition load on a given target species is estimated by the summation (over all other species) of the products of the alphas times equilibrium densities. Each resident species' observed equilibrium population density is then compared to the theoretical population density that a transplanted alien of the same species would achieve if introduced in its place into its community. By this criterion, residents of most species definitely tend to achieve higher population densities than do aliens. Among all 90-odd species over all 30 study areas, residents outperformed aliens in 1871 out of 3014, or 62 percent, of such "experiments." This trend is much more pronounced when expanded food resource matrices are used: in the Kalahari semidesert, when 46 prey categories (including termite castes) are recognized instead of only 20, residents outperform aliens in 810 out of 1056 cases (a full 76.7 percent). In a comparable analysis for two Australian study areas using some 300 different prey resource states, residents outperformed aliens in 39 of 52 possible introductions (75 percent of the time). These results strongly suggest that compensatory interactions are occurring among these naturally coexisting lizard species.
Consider now a second, more complex set of pseudocommunities designed to examine whether or not real communities are organized in various ways. Community ecologists need a way of reducing an entire multidimensional system, or a complex network, to a simple graphical state in which they can appreciate the structure and organization of that entire system. Loehle (1987) said "the mere attempt to define phenomena operationally can dramatically increase theory maturity." Winemiller (1989, 1990, 1991) worked on neotropical fish in South and Central America. Winemiller and Pianka (1990) developed a promising hybrid approach to compare aquatic systems with desert ones. Our approach adopts a holistic perspective on complex assemblages of interacting species and endeavors to represent the entire assemblage graphically to detect patterns of organization in that system.
Raw data for these analyses are also resource utilization matrices. Some reject the whole approach of resource partitioning, but we maintain that a resource matrix contains vital information about a system. It identifies which species eat which other species as well as which species are potential competitors because they share common foods. A resource matrix describes the food web structure of a system.
Considerable tedious work is required to put together a satisfactory resource matrix. Statistical samples of all the species in the system must be collected; if the system is changing in time, this needs to be done quickly; to follow changes in the community through time, adequate samples at different times are necessary. Entries in the resource matrix are used to calculate probabilities, which vary from zero to one, and reflect the probability that a given consumer species will use a particular resource state. Some of these utilization probabilities, uij's, in the matrix will obviously be zeros because some consumers won't be using certain resources. Without going into all the nitty-gritty of the various sorts of probabilistic elements that one can compute to enter into such resource matrices, I want to briefly discuss the concept of electivity.
Simple dietary proportions, or pij's, weight uncommon or very abundant resources disproportionately. Ivlev (1961) suggested resource utilization should be standardized in terms of relative availabilities. Resource availability is not easily measured in the field. Insects can be sampled with sweep nets, DeVac vacuum cleaners, tanglefoot sticky traps, pit traps, or burliese funnels: each technique yields very different results. Some insects are simply more easily pit trapped than others, whereas others are captured by burliese funnels more than others, etc. Pefaur and Duellman (1980; personal communication) studied Andean herps from Colombia to Argentina. They fenced study plots and collected all frogs and squamates (lizards and snakes); inside these plots, all conspicuous insects that a human observer could find were also collected and saved with the intention of using these as standards against the stomach contents of the herps. Humans actually collected only a very few of the insects that were eaten by the herpetofaunas, only about 10 percent (W. Duellman, personal communication). Incredibly enough, 90 percent of the insects that were in stomachs in fact were not even collected by diligent humans! It is a gross and dangerously misleading oversimplification to accept the idea that a single vector of resource availabilities exists that describes a system. Each species experiences its own resource availabilities that depend to some extent on that species' use of space and time as well as its sensory capacities, behavior, and foraging mode.
Various solutions to this problem have been proposed. Colwell and Futuyma (1971) suggested a technique that weights resources in proportion to their use in the overall system. We use a variant proposed by Lawlor (1980a) exploiting the resource totals in the resource matrix as a measure of resource availability. This constitutes a sort of a bioassay. In a system of a hundred species, the diet summed over all the component species represents an estimated resource availability vector. This is used to compute probabilistic analogues of electivity and an analysis can proceed that is unbiased by resource availability.
In a classic paper, Inger and Colwell (1977) pointed out that there is no consensus as to how to approach community ecology, asserting that there is "no standard protocol for community ecology." That statement is still true today, decades later. Even so, in this paper, Inger and Colwell (1977) made a giant step. They suggested a nearest neighbor approach to look at communities, ranking each species' overlap with every other species from the closest neighbor in niche space to those increasingly more distant. Monotonically declining curves for all the species in the system are generated. Some species have high overlap well out into niche space whereas overlap in others falls off rapidly (such consumers are very distinct with low overlap with most of the other members of the system). The hybrid approach Winemiller and I came up with uses simply the mean overlap at a given rank across all species in the system. Figure 17.14 depicts a system in the Kalahari desert with 15 species of lizards. This system will be represented again below, but with a single curve that is simply the arithmetic average over all 15 species at each rank in niche space.
-
Figure 17.14. Plots of dietary overlap with niche neighbors ranked for each lizard species at Tsabong, Botswana. Dietary overlap declines at more distant ranks, but average slopes exhibit large interspecific variation. Overlap at distant ranks is variable in this lizard system. Steep negative slopes indicate relatively unique diets and ecological similarity with very few other species, whereas shallow slopes indicate high or intermediate ecological similarity with many other species. [From Winemiller and Pianka (1990).]
Another promising technique involves null models (Colwell and Winkler 1984). One of the big challenges is to find something with which to compare a given community. It is extremely difficult to compare a system with someone else's system: this provoked us to devise techniques to compare tropical fish with desert lizards. Sale (1974) suggested scrambling the elements of a resource matrix according to some rules to create what I have since come to call pseudocommunities; these are then compared with the original prototype to look for differences to see how the original system is in fact organized. Sale's algorithm involved scrambling all the utilization coefficients, whatever their values are for each consumer in the system (zeros or positive). So one simply takes the first consumer and randomly rearranges all its elements. Rearranged utilization probability u11 could fall with equal probability into any slot in that species' utilization vector as could u21, u31, etc. With a computer, one can easily perform such a rearrangement a hundred times, using a bootstrap approach and exploit Monte Carlo statistics to generate a distribution against which the observed can be compared (Felsenstein 1985; Pimm 1983). Thus one can actually do some statistics and say whether or not any differences are significant.
Lawlor (1980b) suggested a slightly different algorithm
which turns out to be equally instructive: Lawlor's algorithm leaves the zero structure of the
resource matrix intact. If consumer 1 does not eat resource state 3, a zero must remain in cell
u31; it is frozen and not allowed to change. Elements in the resource matrix are
scrambled but only among resources that are actually used by a given species. (We call Lawlor's
method the "conserved-zero" approach and Sale's method the "scrambled-zero"
algorithm because it destroys the zero structure.) Note that both methods retain observed
uij's and hence conserve niche breadth.
To exploit these techniques on our real fish and lizard
systems (Winemiller and Pianka 1990), we constructed a test set of hypothetical model systems that
had understandable known structure. We built model systems both with and without guilds and "
bench tested" our methodology on these (Figure 17.15). Three systems of two guilds of equal
size were constructed with five species in each guild, simple little model systems just to see how
the randomization algorithms affect them. When zeros are scrambled, guild structure is destroyed
and the result is that the scrambled-zero algorithm results in increased overlap at distant ranks
in the niche space. Effectively they sink at close-in ranks and float at distant ranks, because
the original system (the prototype) had niche segregation in it which was destroyed when the
resource matrix elements were scrambled. We also assembled another set of three systems with guilds
of different sizes; these behaved somewhat the same. We also put together systems like these
without any guild structure, but with resource partitioning. It became harder to get pseudocommunities
to differ from their real prototypes, although some conserved zero pseudocommunities did, which we
interpreted as evidence of niche segregation.
Figure 17.15. Plots of average niche overlap against rank of niche
neighbor for three model assemblages with guild structure, and the same plots using means from
100 randomizations based on two algorithms. [From Winemiller and Pianka (1990).] We were also
interested in the phenomenon of core resources. Both Winemiller's fishes and my lizards exploit
certain core resources extensively. Among lizards, these are termites and ants, especially termites. Among fish, mayflies constitute a core resource. So we created other systems with extensive or total overlap on certain core resources and then unique resources used by each species that were partitioned between species.
Summing up bench tests on the effects of these algorithms: When consumers are piled up on a certain resource state (core resources or guilds with all consumer species within a guild eating the same foods), pseudocommunities generated using the scrambled-zero algorithm display lower overlap than observed real systems (i.e., they tend to "sink" because they fall below the observed). But, when resources are partitioned, overlap in randomized conserved-zero pseudocommunities is high, and they tend to be above the observed system (i.e., they "float").
Winemiller studied ichthyofaunas of aquatic systems in Venezuela and in Costa Rica. One of his study sites had more than 80 species of fish in it over the course of an entire annual cycle. Winemiller discovered how to collect virtually an entire freshwater aquatic assemblage. One seine haul during the dry season captured over a thousand fish of dozens of species (plus a "bonus" of a couple of large caiman!)
Winemiller's sample sizes are on the order of 300 to 500. He could not examine the stomachs of all these fish, but went through statistical subsamples and separated his data into wet versus dry season resource matrices. Prey content by volume was estimated to the finest discriminatory abilities possible, given our own expertise, usually insect orders.
We examined 18 different resource matrices, with two or three from each of eight sites: a wet and dry season for each of four fish sites plus microhabitat and diet matrices for each of four lizard sites. Numbers of fish species on these sites vary from 19 to 59 and numbers of lizard species vary from 15 to 39. Between 15 and 217 resource states were represented among sites analyzed.
An Australian desert site, the L-area near Laverton, Western Australia, has 35 species of lizards. My favorite study area is Red Sands, near Yamarna Homestead in Western Australia. I have collected 54 species of lizards there so far and expect to find a few more. The hummock grass tussock plant growth form (spinifex) is very important in the Australian desert. These tussocks, as large as a meter in diameter, house certain lizards that virtually never leave them. Some lizards are highly adapted to spinifex and swim through it with ease. Each lizard collected, some 3000 in Australia and another 2000 from the Kalahari, was weighed and measured in the field, individually tagged, and then permanently preserved by injection with formaldehyde. These specimens are all safely deposited in major museums where they are valuable material for systematics research. Many of these specimens have been used for systematic work and/or dissected by people interested in functional anatomy. When the lizards are returned eventually to the laboratory, each lizard is measured -- ten different body measurements are made on them for anatomical analyses, and then each lizard is dissected and its reproductive state is noted, and relative clutch mass is estimated (testicular cycles can be deduced from serial samples like this), but the most important thing for present purposes is that stomachs are pulled. A competent entomologist went through the stomach contents on the Australian lizards, identifying 100,000 or more prey items to the finest categories possible.
Venezuelan fish assemblages are shown in Figure 17.16 during two seasons, wet and dry, based on two different resource matrices (some fish species present in the wet are not there during the dry season). Mean overlap in the observed system is shown in the upper panel of each graph with solid circles. Overlap at each rank in niche space is plotted, using the average similarity between consumers at the first rank, second rank, third rank, and so on. Pseudocommunities are shown with open symbols, conserved zeros are open circles, and the scrambled zeros are open triangles. In the lower panels of each figure, the percentage of pseudocommunities that either float or sink are plotted. In this case, sinking of the scrambled-zero pseudocommunities indicates guild structure, and floating of conserved-zero pseudocommunities reflects niche segregation. Dashed lines in the bottom panels represent 5 percent and 95 percent confidence levels, so when a pseudocommunity lies above the upper dashed line or below the lower dashed line, there is a statistically significant difference between the pseudocommunities and the observed system. At close ranks in niche space, conserved-zero systems don't float but farther out they clearly differ from observed systems and to some extent, except for the lower right panel in the figure, scrambled-zero psuedocommunities almost invariably sink, at most ranks. In these figures, an enormous amount of information is consolidated into one graph. In one case, at Maraca (top panel), 29,000 fish went into preparation of the figure. Winemiller lived down there for a full year, collected many thousand fish, brought them back, and spent an entire year going through vast numbers of stomachs. All this information can be represented on a single page with a simple graph that one can examine and interpret with a little bit of training. Moreover, very different systems, such as neotropical fish and desert lizards, can be compared with relative ease.
In Costa Rica, fish don't float and sink quite as well as they do in Venezuela, an indication that these central American ichthyofaunas are not as highly organized as the Venezuelan ichthyofaunas.
These aquatic systems are highly organized, with guild structure, core resources, plus niche segregation. Consumers are piled up on certain core resources, reflected in the sinking of the scrambled-zero pseudocommunities. But those same consumers are also segregated out on those core resources that they do use, with different species using the same core resources but with different probabilities.
-
Figure 17.16. Average observed dietary overlap plotted against rank of niche neighbors for two Venezuelan fish assemblages during wet and dry seasons. [From Winemiller and Pianka (1990).]
Australian lizards are depicted in Figure 17.17. At the very top are microhabitats, in the middle are standard dietary resource matrices (19 prey categories, largely insect orders). At the bottom are expanded dietary resource matrices with 201 different prey categories represented at Redsands and 217 prey categories recognized at the L area on the right. Some interesting things emerge from these plots. Scrambled-zero pseudocommunities tend to sink in all cases, which indicates piling up on certain core resources and is indicative of guild structure. Conserved-zero pseudo-communities float pretty well in microhabitats, which indicates niche segregation: different species use different microhabitats and they float fairly unequivocally, except at the closest ranks at Laverton. In the middle plot, though, pseudocommunities do not show very much floating because food resource states are too crudely differentiated, resulting in a piling up of consumers on some resource states. The same data are shown in the bottom panel, but with finer

-
Figure 17.17. Plots of average observed overlap in microhabitat (top) and diet (middle) for 19 condensed prey resource states and (bottom) detailed prey categories against rank of niche neighbors for two Australian lizard assemblages. [From Wine-miller and Pianka (1990).]
discrimination of prey resource states: note that conserved-zero pseudocommunities float as they did in the fish, indicating segregation. Kalahari desert systems are more loosely organized than those in the Australian desert. There are fewer lizard species in the Kalahari and prey could not be distinguished to categories as fine as those in Australia: only 46 different prey resource states were recognized. For microhabitats, there is some hint of floating in the conserved-zero pseudocommunities at Tsabong, Botswana, but not at Bloukrans, South Africa. There is not much niche segregation in diet. There isn't any at all at Tsabong, but there seems to be a little, at least at more distant ranks, at Bloukrans. All in all, the systems we examined tend to be fairly highly organized. This technique should facilitate analyses of other systems and allow comparisons with our own. The pseudocommunity approach is pregnant with potential and would seem to be limited only by our own ingenuity.
Landscape Ecology and Macroecology
The importance of spatial scale has long been neglected in traditional ecology, although not in the emerging field of landscape ecology. While implications of landscape on ecology have always been appreciated, only recently have quantitative methods of study begun to be exploited. In the past, most ecologists, including myself, have focused on local-level processes. Larger scale regional factors also control local phenomena. Local species richness may often be a consequence of regional processes. Relatively little empirical attention has been given to interaction between these two levels.
A recent branch of ecology, known as landscape ecology, is concerned with understanding how species and communities persist within a large geographic region. Landscape ecologists adopt a holistic approach and are interested in such things as the origin, size, and shape of habitat patches, habitat fragmentation, and the role corridors play in facilitating dispersal and hence maintaining viable metapopulations. Satellite imagery offers a powerful new tool for such analyses. To illustrate this approach, I briefly describe some of my own work in progress on the fire succession cycle in inland Western Australia (Pianka 1992, 1994, 1996). Few complete closed regions remain unfragmented by human activities in which regional and local phenomena can still be studied simultaneously. The Great Victoria Desert of Western Australia is an extensive uninhabited area with an extremely high diversity of lizards.
Fires were once a major agent of disturbance in all grassland and semidesert biomes, including North American tall grass prairies. Most of these ecosystems have now been reduced to mere vestiges, and controlled burning and/or fire control are practiced by humans almost everywhere. The inland Australian desert is one of the last remaining areas where wildfires remain a regular and dominant feature of an extensive natural area largely undisturbed by humans. An important fire succession cycle, which generates spatial and temporal heterogeneity in microhabitats and habitats, is evident in this region. These regional processes promote local diversity. This system is being studied at the local level in the field in Australia and at the regional level at the University of Texas using aerial photos and multispectral satellite imagery. High-resolution satellite imagery of these areas, which has been collected since 1972, offers a powerful way, heretofore underutilized, to acquire regional level data on the frequency and phenomenology of wild fires, and thus the system-wide spatial-temporal pattern of disturbance.
Digital satellite data acquired by Landsat has been analyzed in a region covering about 35,000 km2 over a 20 year period to detect burned areas. Spectral and spatial statistics have been computed for 817 fires through time, and the probability that a given area will burn has been estimated. Other data collated for each fire include date, location, area, perimeter, compass direction (of fire scar), ground cover characteristics, extent of laciniation, as well as various fractal dimensions. Age and size distributions of burn patches have been estimated. Supporting imagery from other grassland areas, particularly the Kalahari semidesert of southern Africa, should be acquired and used for comparative purposes (fires in the Kalahari do not appear to reticulate to as great an extent as they do in Western Australia).
A controlled burn was conducted at one mature spinifex (native porcupine grass) site selected for long-term monitoring. Field work on the ground has documented spinifex coverage, vegetation structure has been mapped, and the presence of various animal species, as well as their abundance, have been assessed at various stages following burns. Low-level aerial photography has been acquired and digitized, geo-referenced, and analyzed to make detailed maps of vegetation structure for use in computer simulations of fire dynamics. Vertebrate faunas and insects, particularly foods eaten by lizards, at recently burned sites are being compared with those at various stages of post-fire recovery to describe the dynamics of the fire succession cycle. "Burns" have been simulated on the computer to mimic observed fire geometry. Wind direction and velocity data for 20 years have been analyzed. Precipitation, rates of accumulation of combustibles, and the insect and vertebrate faunas were monitored for two decades to collect data on events occuring during the fire succession cycle.
A major goal of this study is to obtain baseline data on temporal patterns, spatial structure, and distribution of disturbances. These data will form the backdrop for a more detailed study of the population dynamics and dispersal abilities of species. Such data on the component species will be fitted into the overall spatial-temporal habitat mosaic in an effort to explain the persistence of this diverse desert fauna.
Ultimately, we plan to model the entire Great Victoria Desert region as a dynamic patchwork of habitats to aid in understanding mechanisms of coexistence of its component species and the effects of fire disturbance in maintaining lizard diversity in this landscape.
An even larger, macroscopic, continent-wide perspective has been adopted and deemed "macroecology" by Brown and Maurer (1989) and Brown (1993). Body masses of entire continental faunas are distributed lognormally; however, size distributions within a given habitat are considerably flatter (Figure 17.18), presumably due to interspecific competition. Brown and Maurer argue that small species are more specialized and
-
Figure 17.18. Frequency distributions of body masses among species of North American land birds (a) and mammals (b) for the entire continent, for land mammals within biomes (c, d), and for land mammals within small patches of uniform habitat within biomes (e, f). [From Brown and Maurer (1989).]
have smaller geographic ranges and replace each other more frequently as one moves across the landscape than larger species (which generally have broad geographic ranges). A threshold body mass occurs at around 100 grams (Figure 17.19). Up to this critical threshold, species are able to compensate for the higher costs of being smaller by increasing food requirements per unit area of territory. However, average population densities fall as body sizes are reduced below about 50 to 100 grams. Population densities of large animals also tend to be lower than those of moderate-sized animals (Figure 17.19). Large species use more energy than small ones, both on a per species basis and for all species within a size category (Figure 17.20).
-
Figure 17.19. Relationship between average population density and body mass for species of North American land birds. Various hypothesized constraining factors are indicated with dashed lines. [From Wiens (1989) after Brown and Maurer (1989).]
-
Figure 17.20. Relative energy usage plotted against body masses for North American land birds. (a) Average values for species, and (b) values summed for all species in various logarithmic size classes. [From Brown and Maurer (1989).]
In both North American terrestrial mammals and land birds, long axes of geographic ranges tend to be oriented north-south in small species but east-west in large ones (Figure 17.21). However, in Europe, ranges of species of all sizes are aligned east-west. Brown and Maurer offer the following reasonable explanation for these patterns. Species with small ranges (and mostly small body sizes) are limited by habitat types and major topographic features, such as mountain ranges, river valleys, and coast lines. These are oriented predominantly north-south in North America, but east-west in Europe. Species with large ranges are relatively insensitive to such variables and are instead limited by major climatic zones and biome types that are arranged east-west.
-
Figure 17.21. Maximum north-south and east-west extent of geographic ranges of North American terrestrial mammals (a) and land birds (b). (c) The same plot for European land birds. [From Brown and Maurer (1989).]
In a study across a broad range of spatial and temporal scales, Holling (1992) concludes that landscapes are structured hierarchically by a relatively small number of structuring processes into a small number of levels, each characterized by a distinct scale of "architectural" texture and of temporal speed variables. Each of the small number of processes influencing structure operates over a limited range of scale (Figure 17.22).
-
Figure 17.22. Two examples of how elements of ecosystems scale in time and space. (a) Scaling in the boreal forest. (b) Scaling in the hierarchy of decisions made by large wading birds. In both plots, time is measured in years and space in kilometers. [From Holling (1992).]
In addition, Holling claims to have found evidence that nature is "lumpy," with distinct gaps occurring between such patches of structure. The temporal and architectural structure of ecosystem quanta are determined by three broad groups of processes, each dominating over different ranges of scale. Due to the nonlinear nature of disturbance processes at intermediate ("meso-") scales, fine-scale knowledge of autecology cannot be aggregated to represent behavior at scales beyond the scale of a patch or gap (Holling 1992).
Selected References
Systems and Macrodescriptors
Diamond and Case (1986); Inger and Colwell (1977); Kikkawa and Anderson (1986); Levins (1968); Motomura (1932); O'Neill et al. (1986); Orians (1980a).
Systems Ecology
Berryman (1981); Bertalanffy (1969); Bormann and Likens (1967); Caswell et al. (1972); Chorley and Kennedy (1971); Clark et al. (1967); Dale (1970); Foin (1972); Forrester (1971); Holling (1959a, b, 1963, 1964, 1965, 1966); Hubbell (1971, 1973a, 1973b); Huffaker (1971); Kitching (1983b); H. Odum (1971); O'Neill et al. (1986); Patten (1971, 1972, 1975, 1976); Reichle (1970); Waterman (1968); Watt (1966, 1968, 1973); Weinberg (1975).
Compartmentation: Trophic Levels
Adams et al. (1983); Allee et al. (1949); Briand and Cohen (1984); Carney et al. (1981); Cohen (1978); Cousins (1985); Elton (1927, 1949, 1966); Gallopin (1972); Hubbell (1973a, 1973b); Kozlovsky (1968); Leibold et al. (1997); Murdoch (1966a); Odum (1959, 1963, 1971); Paine (1966); Phillipson (1966); Pimm (1979, 1980, 1982, 1984); Pimm and Lawton (1977, 1980).
Compartmentation: Guild Structure
Holmes et al. (1979); Inger and Colwell (1977); Joern and Lawlor (1981); MacMahon (1976); Pianka (1980); Pianka, Huey, and Lawlor (1977); Rathcke (1979); Root (1967); Terborgh and Robinson (1986); Ulfstrand (1977).
Compartmentation: Food Webs
Armstrong (1982); Auerbach (1984); Briand (1983); Briand and Cohen (1984); Cohen (1978); Critchlow and Stearns (1982); Hairston, Smith, and Slobodkin (1960); Paine (1966, 1977, 1980, 1983, 1988); Pimm (1979, 1980, 1982, 1984, 1991); Polis and Winemiller (1996); Polis et al. (1997); Schoener (1989); Winemiller (1989, 1990); Yodzis (1980, 1981, 1988).
The Community Matrix
Lane (1985); Lawlor (1980); Levine (1976); Levins (1968); May (1973); Neill (1974); Parker and Turner (1961); Pianka (1987); Seifert and Seifert (1976); Vandermeer (1970, 1972a, b, 1980).
Biogeochemical Cycles in Ecosystems
Boorman and Likens (1967); DeAngelis (1980); Hutchinson (1950); Meili (1995); Pimm (1982); Whittaker (1975); Vitousek and Sanford (1986).
Principles of Thermodynamics
Bertalanffy (1957); Brody (1945); Gates (1965); Odum (1959, 1971); Phillipson (1966); Wiegert (1968).
Pyramids of Energy, Numbers, and Biomass
Elton (1927); Leigh (1965); Odum (1959, 1963, 1971); Phillipson (1966); Slobodkin (1962a).
Energy Flow and Ecological Energetics
Bertalanffy (1969); Boorman and Likens (1967); Engelmann (1966); Gates (1965); Golley (1960); Hairston and Byers (1954); Hubbell (1971); Lindemann (1942); Mann (1969); Margalef (1963, 1969); Odum (1959, 1963, 1968, 1969, 1971); Oksanen and Oksanen (2000); Paine (1966, 1971); Patten (1959); Phillipson (1966); Polis and Strong (1996); Reichle (1970); Schultz (1969); Slobodkin (1960, 1962a); Teal (1962).
Secondary Succession
Anderson (1986); Bazzaz (1975); Clements (1920); Drury and Nisbet (1973); Horn (1971, 1974, 1975a, b, 1976, 1981); Hutchinson (1941); Margalef (1968); Otte (1975); Pickett (1976); Usher (1979); Watt (1947).
Evolutionary Convergence and Ecological Equivalence
Grinnell (1924); MacArthur and Connell (1966); Pianka (1985); Raunkaier (1934); Recher (1969); Salthe (1972).
Community Evolution
Darlington (1971); Dunbar (1960, 1968, 1972); Futuyma (1973); Lewontin (1970); Odum (1969); Ricklefs and Cox (1972); Rummell and Roughgarden (1985); Whittaker (1972); Whittaker and Woodwell (1971).
Pseudocommunities
Caswell (1976); Colwell and Winkler (1984); Gotelli and Graves (1996); Joern and Lawlor (1980); Lawlor (1980); Pianka (1986); Sale (1974); Sanderson (2000); Sanderson et al. (1998); Winemiller and Pianka (1990).
Landscape Ecology and Macroecology
Brown (1993); Brown and Maurer (1989); Forman and Godron (1986); Haydon and Pianka (1999); Holling (1992); Maurer (1999); Pianka (1993); Ricklefs (1987); Wiens and Milne (1989).
|

