19| Island Biogeography and Conservation Biology

Ecosystems are usually difficult to manipulate experimentally; hence, much of modern ecology has had to rely on exploitation of "natural" experiments -- situations in which one (or a few) factor(s) affecting a community differ between two (or more) ecosystems. For this reason, ecologists have long been especially interested in islands, which constitute some of the finest natural ecological experiments. Different islands in an archipelago often contain different combinations of the mainland species, allowing an investigator to observe both ecological and evolutionary responses, such as niche shifts, of various component species to the presence or absence of other species (Figure 19.1).

Figure 19.1. Observed and expected frequency distributions of perch heights of Anolis lizards. (a) Observed height distribution of A. carolinensis where it occurs on an island alone without competitors. (b) Expected distribution of perch heights of A. carolinensis on another island with different availabilities of various perch heights, assuming no niche shift. (c) Observed distribution of A. carolinensis on the second island with a competitor [compare with (b)]. (d) Height distribution of perches of the competing species, A. sagrei. [From Schoener (1975a).]

Islands can be exploited as natural ecological experiments in numerous other ways as well. Thus, because islands support fewer predatory species than comparable mainland habitats, they can be used to study the effects of predator exclusion. Moreover, reduced species densities on islands, such as the land birds of Bermuda, allow partial analysis of the effects of interspecific competition on the ecologies of those species that have populated an island.

Islands of a sort are widespread in the terrestrial landscape, too; a patch of forest separated from a larger stand of trees can be considered a "habitat island." Similarly, isolated lakes and mountaintops represent "islands." To a nonflying insect, plants in the desert or trees within an open forest may approximate islands in that they are separated from one another by relatively vast open spaces of a different and relatively inhospitable environment. Likewise, cattle droppings scattered about a field are islands to the animals that inhabit them (Mohr 1943). Hosts are islands to their parasites. Even a drop of water or the body of an insect may be an island to a bacterium.

Species-Area Relationships

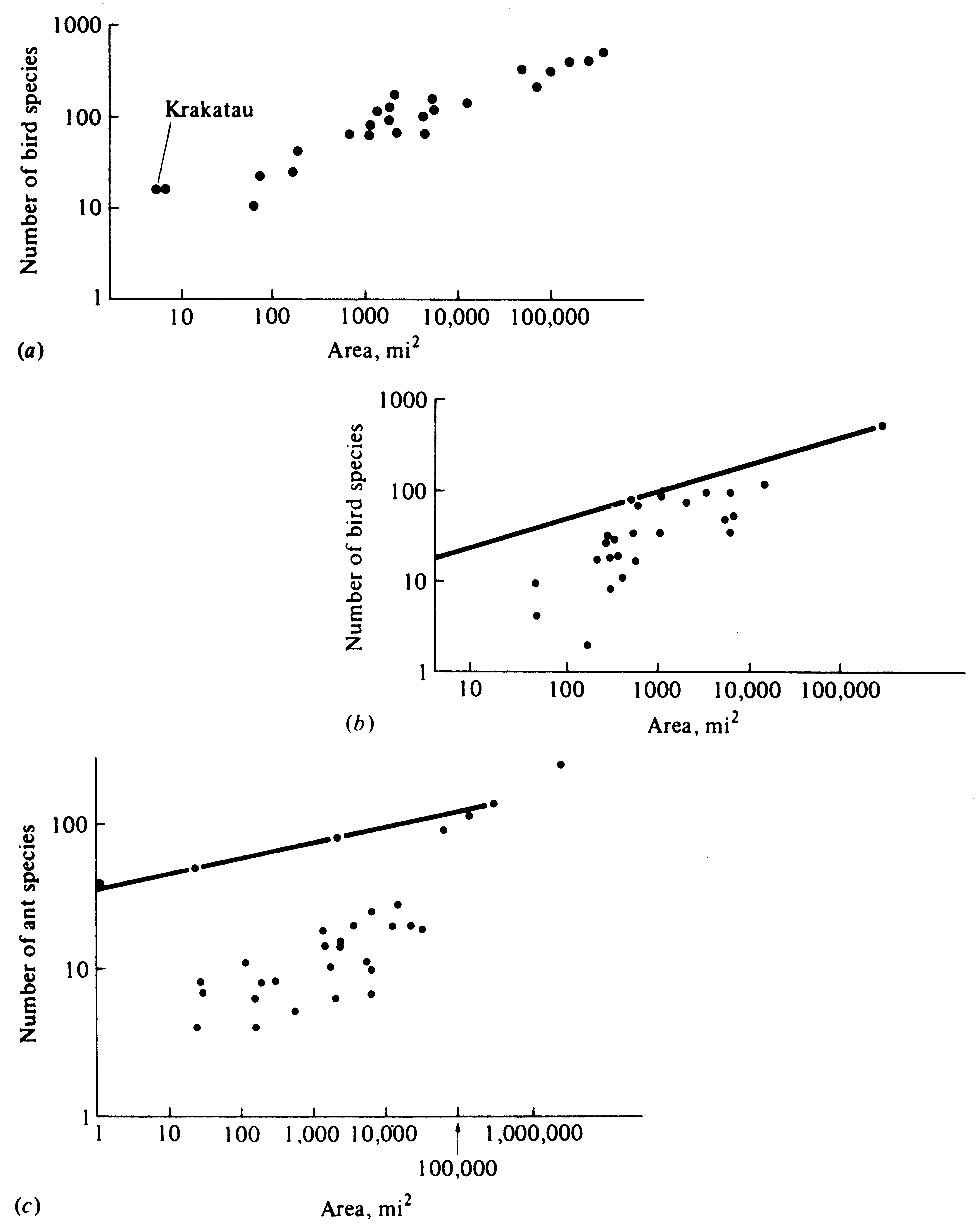
Larger islands generally support more species of plants and animals than smaller ones. In fact, when plotted on a double log scale, the number of species in a given taxon typically increases more or less linearly with island size (Figure 19.2). In most cases, a tenfold increase in area corresponds to an approximate doubling of the number of species. The slope of a linear regression line through such points is designated as that taxon's z-value in the particular island system. In a variety of taxa on many different island systems (Table 19.1), z-values generally range from about 0.24 to about 0.33. The z-value is the exponent in the equation

S = CA ^z (1)

where S is the number of species, C is a constant that varies between taxa and from place to place, and A is the area of the island(s) concerned. Taking logarithms and rearranging, one obtains a linear equation in which z is the slope:

logS = logC + z logA (2)

Large values of z result from topographic diversity and spatial replacement of species, or "islands within islands"; lower values arise with reduced replacement of species in space, as on very homogeneous islands, continents, or subsamples of large islands (see subsequent discussion). Area in itself is probably not the primary factor affecting species density in most situations, but it presumably operates indirectly through increasing the variety of available habitats. However, area can directly affect species densities in some situations.

Figure 19.2. Various species-area relationships. (a) Numbers of species of land and freshwater birds on islands of the Sunda group in southeast Asia, with the Philippines and New Guinea. Krakatau is plotted at the extreme left. (b) Numbers of species of land and freshwater birds on various often remote islands in the South Pacific, including the Moluccas, Melanesia, Micronesia, Polynesia, and Hawaii. The line is drawn through the two islands (Kei and New Guinea) nearest to source regions to demonstrate the degree of departure of species densities on the more remote islands. (c) Number of species of ponerine ants in the faunas of various Mollucan and Melanesian islands. The line represents the number of species with increasing area in subsamples of New Guinea; points represent smaller islands. Note that the islands support fewer species than a comparable sized portion of New Guinea but that the rate of increase of species with area is greater among the islands than it is within New Guinea. [(a, b) From MacArthur and Wilson (1967). The Theory of Island Biogeography. Copyright © 1967 by Princeton University Press. Reprinted by permission of Princeton University Press. (c) From Wilson (1961).]

Table 19.1 Estimated z Values for Various Terrestrial Plants and Animals on Different Island Groups

__________________________________________________________________

Fauna or Flora Island Group z

__________________________________________________________________

Carabid beetles West Indies 0.340

Ponerine ants Melanesia 0.300

Amphibians and reptilesWest Indies0.301

Breeding land and freshwater birdsWest Indies 0.237

Breeding land and freshwater birdsEast Indies0.280

Breeding land and freshwater birdsEast-Central Pacific0.303

Breeding land and freshwater birdsIslands of Gulf of Guinea0.489

Land vertebratesIslands of Lake Michigan0.239

Land plants Galápagos Islands 0.325

__________________________________________________________________

Source: From MacArthur and Wilson (1967).

An area of mainland habitat comparable to and equal in size to an offshore island almost invariably supports more species, especially those at higher trophic levels, than the island does. The number of species in samples of a continental system also increases with the size (area) of the subsample, although not as rapidly as on islands (Figure 19.2). Typically, z-values in mainland situations range from about 0.12 to about 0.17. This difference arises because an island is a true "isolate," whereas a similar sized patch of mainland habitat is only a "sample"; rare species can occur in the mainland sample both due to migration from other areas and because areas immediately adjacent to the subsample also support other members of broad-ranging species. A mountain lion requiring a 20-km² territory would be unlikely to maintain a viable population on a small island of, say, less than 30 to 40 km², whereas these same cats are able to survive and replace themselves in a similar sized subsample of a larger landmass. This is why islands tend to support fewer species at higher trophic levels than mainland areas do.

Equilibrium Theory of Island Biogeography

For many years, islands were considered to be in some sense "impoverished" of species both because of the obvious problems species have in colonizing them and because islands typically support fewer species than a comparable area of mainland habitat. However, the regularity of species-area patterns led MacArthur and Wilson (1963, 1967) to examine the possibility that islands might in fact be supporting as many species as possible [this idea was first considered by Munroe (1948)].

MacArthur and Wilson reasoned that the rate of immigration of new species to an island should decrease as the number of species on that island increases. The immigration rate must drop to zero as the species density of the island reaches the total number of species in the "species pool" available for colonization of the island at which no immigrant can be a new species. (The species pool corresponds to the total number of species in source areas surrounding a particular island system.) MacArthur and Wilson argue that the rate of extinction of species already present on an island should increase as the number of species on an island increases; this seems likely because as more species invade an island, average population size must decrease and both the intensity of interspecific competition and the incidence of competitive exclusion should increase. Moreover, there are more species to go extinct.

When the rate of immigration equals the rate of extinction (Figure 19.3), existing species go extinct at the same rate that new ones invade; thus, species density reaches a dynamic equilibrium. Although species density stays constant, the continual turnover of species means that the actual composition of species on an island can be changing.

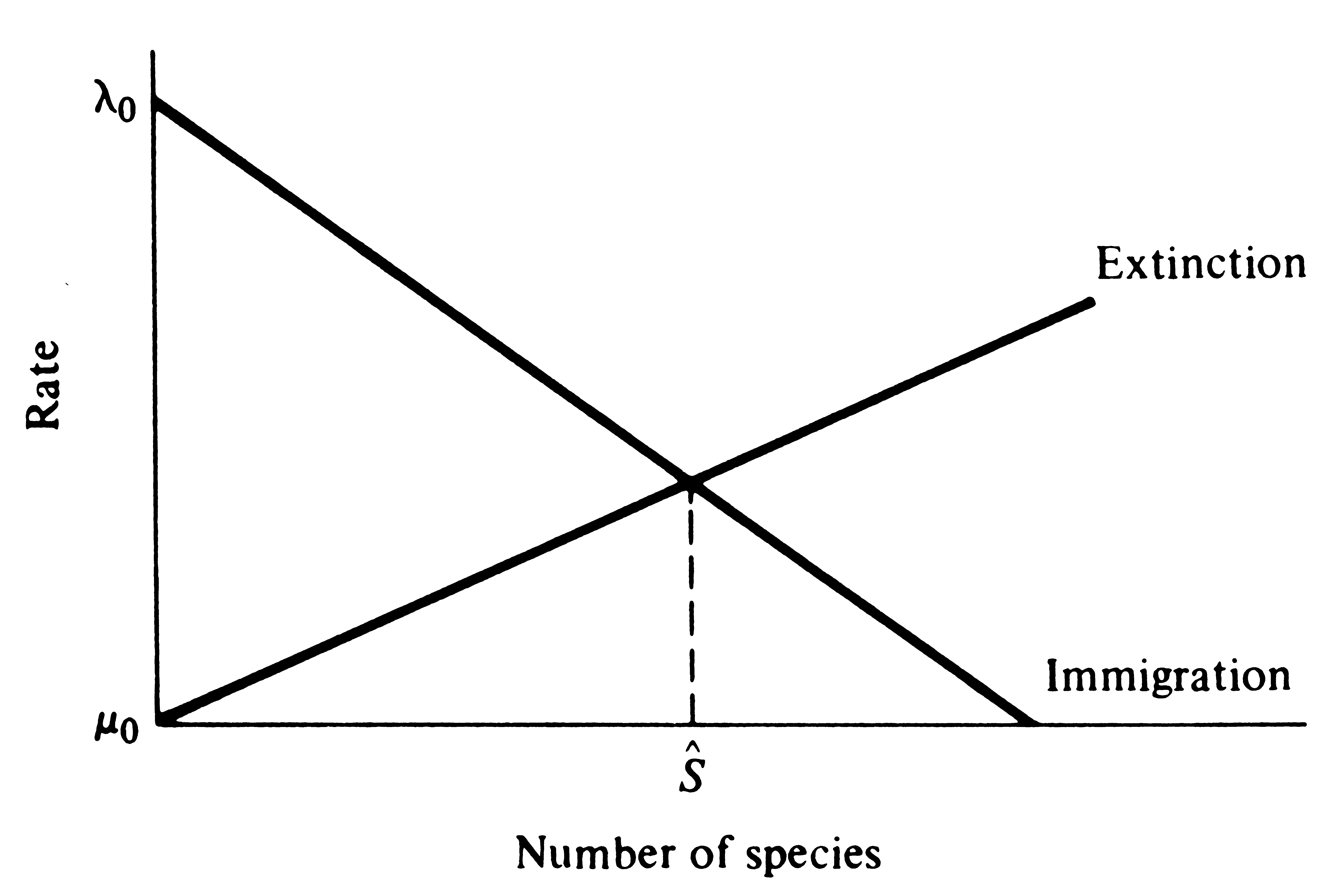
Figure 19.3. Illustration of the equlibrium theory for island species densities, with the immigration rate of new species falling and the rate of extinction of existing species rising
as the total number of species on an island increases. At equilibrium, immigration just balances extinction and S* different species exist on the island. The composition of the island's biota may change as some of the
existing species go extinct and are replaced by other, different species.

MacArthur and Wilson's equilibrium theory is somewhat analogous to the model of the Verhulst-Pearl logistic equation for growth processes within a population (see Chapter 9); thus, number of individuals (density), N, is replaced by the number of species (species density), S, and density-dependent birth and death rates, bN and dN, are replaced by a falling immigration rate, λ, and a rising rate of extinction, μ, as the species density of an island increases. As a first approximation, we might assume that rates of immigration λ and extinction μ vary linearly with species density according to the equations

λS = λ₀ - αS (3)

μ_S = βS (4)

where λ₀ is the rate of immigration with no species present on the island and α and β represent rates of change in rates of immigration and extinction, respectively, as species density increases (Figure 19.4). [MacArthur and Wilson (1963, 1967) point out that this assumption of linearity is not as stringent as it might at first seem, because transformations of the ordinate may allow simultaneous straightening of immigration and extinction curves.] At equilibrium, Sˆ or S*, the rate of immigration must exactly equal the rate of extinction -- that is, λ_S must equal μ_S. Setting equation (3) equal to (4),

λ₀ - αS* = βS* (5)

and rearranging, one obtains an expression for the number of species at equilibrium

S* = λ₀ /(α + β) (6)

Equation (6) is, of course, identical in form to the expression for carrying capacity K in the logistic equation which is K = r/(x + y) [see also equation (9) in Chapter 9].

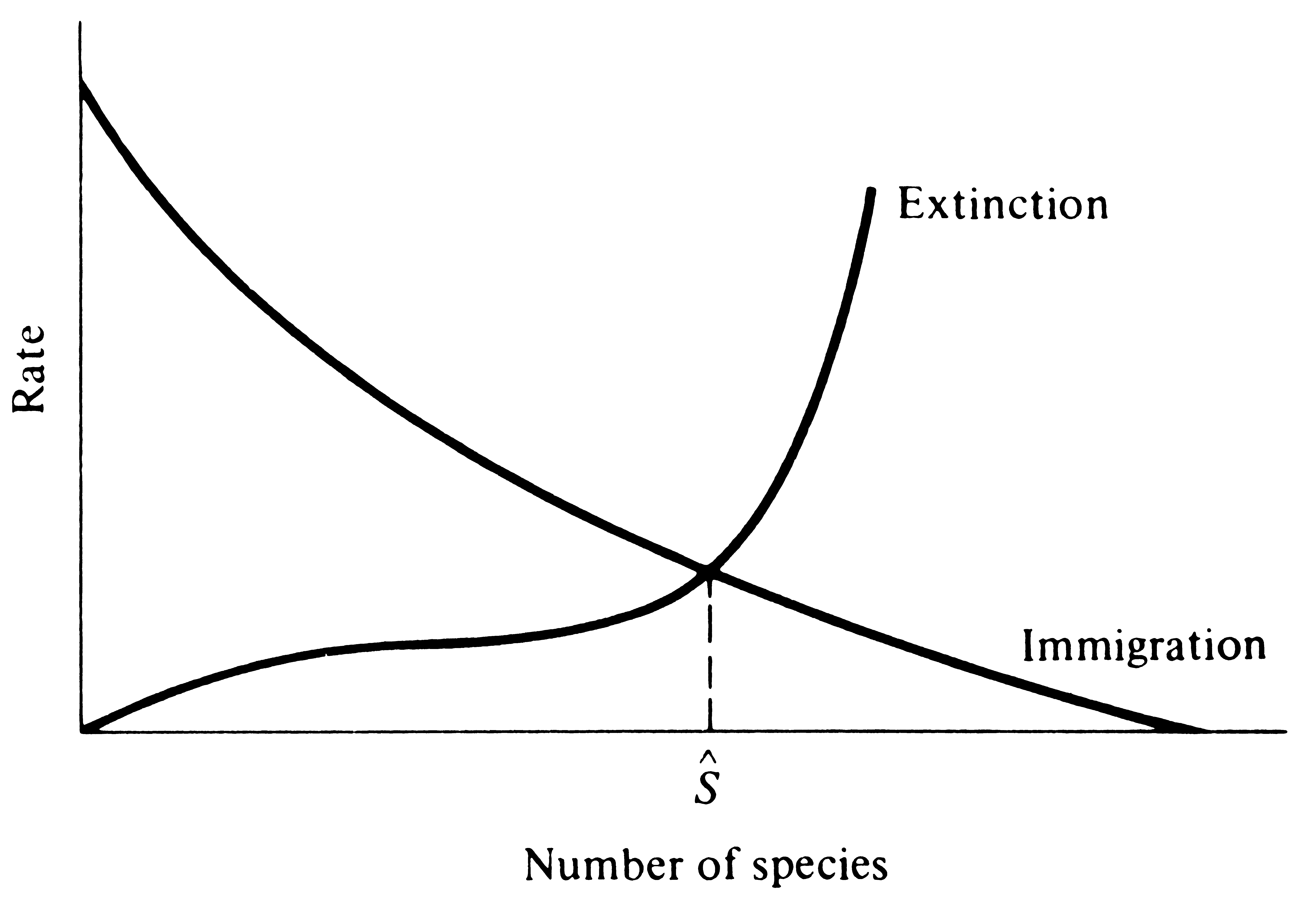
Figure 19.4. Immigration and extinction rates that change linearly with island species density. Equilibrium species density, S*, is a simple function
of the slopes and intercepts of the two lines.

At equilibrium, the total rate of immigration of species must equal the total extinction rate. However, because species going extinct will undoubtedly often differ from those that successfully invade an island, the composition of an island's biota will be continually changing, even at equilibrium.

As previously developed, λ's and μ's represent total rates of immigration and extinction and thus indicate little about the relative rates per species either already present on the island or available in the species pool (P). The average rate of immigration per species, λ, and the average rate of extinction per species, μ, can be obtained by dividing by, respectively, the number of species not yet on the island (P - S) and the number already present on the island (S):

λ= λ_S / (P - S)orλ_S = λ (P - S) (7)

μ = μ_S / Sorμ_S = μ S (8)

Again, at equilibrium, total extinction rate (μ_S) must equal the total rate of immigration (λ_S); that is, λ_S = μ_S, or in terms of the average rates per species (which are the rates with which an ecologist will usually be working):

λ (P - S*) = μS* (9)

Solving for the equilibrium number of species, S*, gives

S* = (λ P) / (μ + λ) (10)

Equation (10) demonstrates that S* increases with increasing P and λ and decreases with increased μ. Notice also that λP is λ₀ [compare equation (10) with equation (6)] and that λ is identical to α in equation (3), whereas μ is β in equation (4).

Figure 19.5. Some actual patterns of dispersal, both vertical and horizontal. The number of organisms decays rapidly at first and then more and more slowly with increasing distance. [From Odum (1959) after Wolfenbarger.]

Because dispersal falls off more or less exponentially with distance (Figure 19.5), MacArthur and Wilson (1963, 1967) reasoned that immigration rates should decrease with increasing distance from source areas (Figure 19.6). Further, they argued that

Figure 19.6. Immigration rates should decrease with increasing distance from source areas so that distant islands should reach equilibrium with fewer species, S_d*, than close-in islands, S_c*, all else being equal. Moreover, turnover rates should also be higher on nearby islands than on comparable but more distant islands (T_c > T_d).

rates of extinction should be largely unaffected by distance from source areas per se but should instead generally increase with decreasing island size because smaller islands support smaller, more tenuous populations (Figure 19.7). [Because they present a smaller "target" for potential invaders, smaller islands might also have slightly lower immigration rates than other equivalent but larger islands. But this change should be minor compared with the expected decline due to the exponential decay in the number of immigrants with distance (see Figure 19.5).] Note also that on islands equidistant from source areas, rates of species turnover should be higher on small islands.

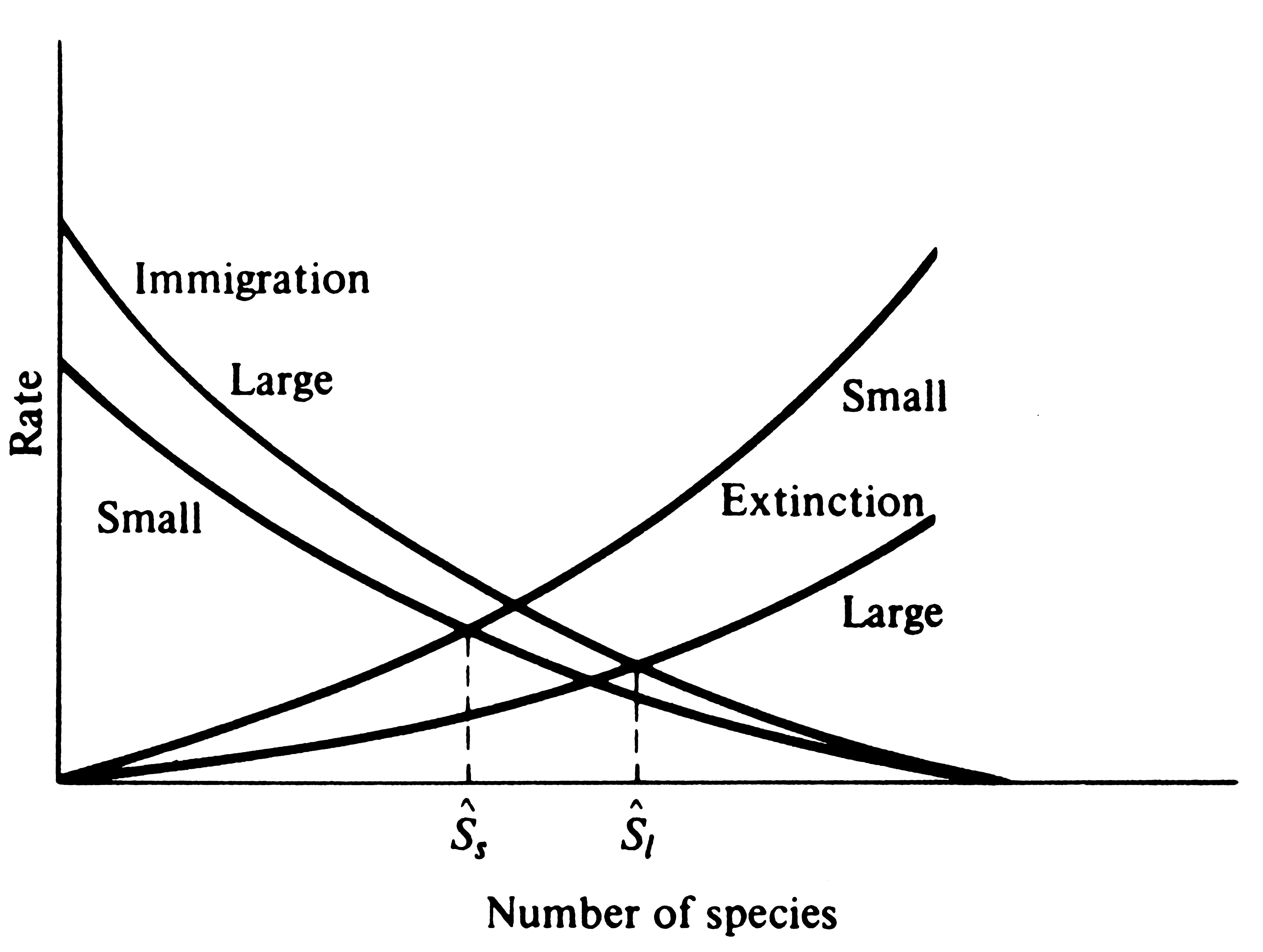
Figure 19.7. Extinction rates should be little affected by distances from source areas, but they should often vary inversely with island size and/or complexity. Immigration rates may also be slightly higher on larger islands because they present a larger "target" for potential invaders. Thus, all else being equal, a small island should equilibrate with fewer species, S_s*, than a larger island, S_l*. Also notice that turnover rate is higher on the small island than on the large one.

than on large ones (turnover rate should thus vary inversely with equilibrium species density). Simple islands with little topographic relief and relatively few different habitats should have generally higher extinction rates than more complex and more diverse islands with a greater variety of habitats, because the latter would provide a greater variety of immigrants with suitable opportunities for successful invasion and persistence on the island. Finally, clumped islands such as archipelagos should have higher rates of immigration than more scattered or isolated islands due to interchanges of plants and animals between islands.

Some predictions of equilibrium theory have now been supported by observations; others, especially those involving turnover rates, have proven to be difficult to test.

Islands as Ecological Experiments: Some Examples

Hawaiian Drosophilidae

The Hawaiian Islands constitute the most isolated archipelago on the earth. They support a truly remarkable natural fauna, unfortunately now seriously disturbed by inane human activities. Among the most interesting of Hawaiian organisms are its famous fruit flies, family Drosophilidae. A diverse group of nearly 800 different species has evolved there, almost certainly from a single common ancestor. These flies are placed in two genera, Drosophila and Scaptomyza, both of which are also found elsewhere in the world, although in greatly reduced diversity. Hawaiian drosophilids have adopted a wide variety of ecological niches; they have diversified into predators, parasites, nectarivores, detritivores, and herbivores -- some are generalists (most larvae eat parts of plants, including leaves, bark, stems, roots, sap, nectar, and fruit), but others are very specialized, frequently to certain specific positions on a single species of host plant. In contrast, one of the generalized species has been found on plants of 21 different families!
Most Scaptomyza are tiny flies 2 mm or less in length, with leaf-mining larvae. Some of the so-called "picture-winged" Drosophila are relatively gigantic flies, measuring up to 7 or 8 mm long (D. cyrtoloma has a wingspread of nearly 20 mm!). Detailed genetic work has allowed construction of a phylogeny for 100 species of picture-winged Drosophila. The islands themselves have been dated by geological means, as they arise over a "hot spot" in the earth's mantle and then drift off to the northwest (the Hawaiian islands become progressively older from the southeast to the northwest). Almost all species of picture-winged Drosophila are endemic to a single island. The most primitive species are in fact found on the oldest islands, while the most derived species occur on the youngest islands.

Many Hawaiian Drosophila have experienced strong sexual selection. Males compete intensely for virgin females, advertising from small territories, sometimes termed "leks" (although these differ from avian leks). Males are very aggressive toward other males and courtship behavior is complex. Reproductive tactics of Hawaiian Drosophila are quite varied; females of some species deposit large numbers of eggs in clusters, others produce many eggs but lay them singly, while females in still other species lay just a single egg per day. This model system clearly invites much more extensive ecological and evolutionary research.

Krakatau

In 1883, the small volcanic island of Krakatau, located between Java and Sumatra, erupted repeatedly over a three-month period. All of Krakatau and two adjacent islands were covered with red-hot lava, pumice, and ash to a depth of many meters. The islands were so hot that months afterward falling rain turned to steam on contact. It is most unlikely that any organisms survived. Repopulation from adjacent Sumatra (about 25 km away) and Java proceeded rapidly and by 1921 the number of resident species of birds was comparable to that expected on a small island of 20 km² (the size of Krakatau after the eruptions) in the general region. The total number of bird species did not change much between 1921 and 1933, although the composition of the avifauna did. This example suggests that mobile organisms such as birds rapidly reach an equilibrium species density. On the other hand, plant species were still being added rapidly in 1934 but had leveled out by 1983 (Figure 19.8).

Figure 19.8. Numbers of plant species recorded on the three islands of the Krakatau group, from 1883 to 1983. Wind-dispersed Spermatophyta (higher plants) and wind-dispersed Pteridophyta (ferns) as well as species dispersed by other means, such as rafting (sea), bird/bats, and humans, are also shown. [From Whittaker et al. (1989).]

The Taxon Cycle

Many island species are thought to progress through a series of evolutionary changes, termed a taxon cycle, that eventually may greatly increase their probability of going extinct (Wilson 1961; MacArthur and Wilson 1967; Ricklefs and Cox 1972). Under this hypothesis, early in the taxon cycle a species is widespread and occurs on many islands, is often in the process of invading new islands, and is only slightly (if at all) differentiated into distinct populations on the various islands. It is adapted to marginal, relatively unstable habitats such as riverbanks and forest clearings. Later in the cycle, populations of a species become progressively more and more differentiated on different islands, at first remaining widespread. At this stage it penetrates more stable habitats, such as old forests, where it must coexist with larger numbers of native species. Still later, after local extinction on some islands, a differentiated species becomes more restricted and its geographic range is fragmented. Finally, species at the end of the taxon cycle are found only on a single island (i.e., they are endemic to one island). Occasionally, some species are able to shift back into marginal, species-poor habitats, thus restarting the cycle. Ricklefs and Cox (1972) argue that the taxon cycle for a particular species is driven by counteradaptations of other members of an island biota against the species concerned. Dispersal ability decreases as species depend less and less on the ability to colonize marginal habitats and more on their capacity to coexist with competing species in stable habitats. Such reduced dispersal and more pronounced local adaptation in turn favors speciation and endemism. Newly arrived colonists are relatively free of a counteradaptive load, allowing them to spread successfully throughout an island system in relatively unstable habitats. On small and remote islands, old populations of endemics, such as the Cocos Island finch, may persist.

Although the taxon cycle may not apply to all species, the concept underlying it presumably could operate in mainland faunas as well as on islands. Little attempt has yet been made to interpret the ecology of mainland populations in terms of such counteradaptations, although the concept of a fugitive species is clearly relevant.

Experimental Biogeography

Deducing biogeographic processes from history is difficult because history is both unique and unknown. The fact that only one history exists makes it impossible to estimate the degree of determinism surrounding the realization of biogeographic processes. Consequently such deductions cannot be generalized. Modern computers have enabled a new approach, known as "experimental biogeography," that models faunal buildup repeatedly against a fixed vicariant background over both ecological and evolutionary time scales. An experimental biogeographer knows both actual vicariant history and the true phylogeny. History can thus be replayed on a computer to accumulate a sample of multiple phylogenies and to estimate probabilities for various biogeographic processes. Roles of stochastic, historical, and ecological processes in adaptive radiations can be assessed. Experimental biogeography also allows the reliability of various methods of recovering probable historical patterns to be assessed. This new approach to biogeography is pregnant with potential, but has just barely begun to be explored.

Conservation Biology

Someone said, "Once humans were surrounded by wilderness and wild animals, but now we surround them." Urbanization and habitat destruction have reduced the populations of almost all non-human species, some to the critical point of near extinction. This book has emphasized basic ecological principles, many of which have obvious and important applications. For example, optimal yield to maximize sustained harvests has long been a goal in wildlife management and fisheries biology. Even so, humans have overfished the world's oceans. Conservation biology is a man-made crisis discipline analogous to surgery in medicine or war in political science. This emerging field seeks to conserve natural habitats and maintain biotic diversity. Biodiversity constitutes a valuable resource worthy of preservation for many different reasons. Consider some anthropocentric ones. Genetic strains of plants with natural resistance to pests are valuable to humans because their genes can be exploited to confer resistance on future crop plants.

Approximately one drug in four originated in a rain forest: these include analgesics, diuretics, laxatives, tranquilizers, contraceptives, and cough drops. Antibiotics were first discovered in fungi, but have now also been found in many species of plants as well. Secondary chemicals of plants have proven to be a vast reservoir for useful pharmaceutical products. Clinically proven drugs derived from higher plants include: morphine, codeine, atropine, quinine, digitalis, and many others. Bark of Pacific yew trees contains taxol, which has proven to be an effective agent in the treatment of certain ovarian cancers. To date, scientists have examined only about 1 percent of existing plant species for useful pharmaceuticals.

Biodiversity is not distributed evenly across earth's surface: only 2% of earth (so-called "hot spots") support almost half the species currently extant (Myers 1988, 1990; Mittermeier et al. 1998). Most of these areas are in the tropics, many in southeast Asia where humans are rapidly encroaching on natural habitats. Archipelagos in Indonesia and the Philippines house many species that are restricted to only a given island (endemic species).

In conservation biology, a debate has arisen about whether it is better to have a single large reserve or several small reserves (the so-called SLOSS debate). Because a single large reserve will support only a single population, if this should go extinct that species will be lost; whereas with several smaller reserves, if a population goes extinct in one, it can still re-invade and re-establish itself from another reserve.

Conservation biologists attempt to estimate the minimum viable population size for endangered species. A minimum viable population is the threshold population size for persistence, one that is just large enough to minimize the probability of extinction from all forms of stochasticity (genetic, demographic, and environmental) over a reasonably long period of time. When a population is reduced to a very small size, it must go through a genetic bottleneck, which can greatly reduce genetic variability. Conservation biologists often study the genetics of small populations. Demographic and environmental stochasticity were discussed in Chapter 8. A population viability analysis assesses the current status of a species and systematically determines the conservation measures needed to prevent its extinction. Leslie matrices (Chapter 8) have been used to identify vulnerable age classes that require protection for persistence of endangered species.

Basic demographic parameters were estimated for the endangered Bonnelli's eagle Hieraaetus fasciatus in Spain and France (Real and Manosa 1997) and a 3 x 3 Leslie matrix was constructed. A sensitivity analysis of these data showed that population growth rate was about four times less sensitive to changes in preadult survival than to changes in adult survival, and about ten times less sensitive to changes in fecundity and predispersal survival than to changes in adult survival. Conservation efforts should therefore be directed toward increasing adult and preadult survival. For the species to persist, mortality must be reduced by reducing or eliminating both power line casualties and direct persecution by humans.

For many species, combined effects of habitat loss, habitat fragmentation, small population size, genetic and demographic stochasticity, toxic pollution, and climatic changes are overwhelming -- Soulé calls the resulting situation an "extinction vortex" which, like a whirlpool, seems to conspire to pull many existing populations down to precariously low densities or even actual extinction.

Metapopulations

Most species are broken up into many subpopulations, isolated from one another to varying degrees depending upon barriers to dispersal and proximity. Such a set of all possible populations is termed a metapopulation (Figure 19.9). Levins (1969) proposed the following simple mathematical model to describe the dynamics of metapopulations:

dp/dt = mp (1 - p) - ep

where p denotes the fraction of habitat patches occupied by the species, e is the per patch rate of local extinction, and m represents the per patch rate of colonization of empty patches. An equilibrium is reached when p is equal to 1 - e/m. This model assumes that all patches of habitat are identical and that the species is either present or absent in any given patch. Moreover, all local populations are assumed to have the same probability of going extinct, and the rate of colonization of empty patches is proportional to the fraction of occupied patches (p) and to the fraction of empty patches (1 - p).

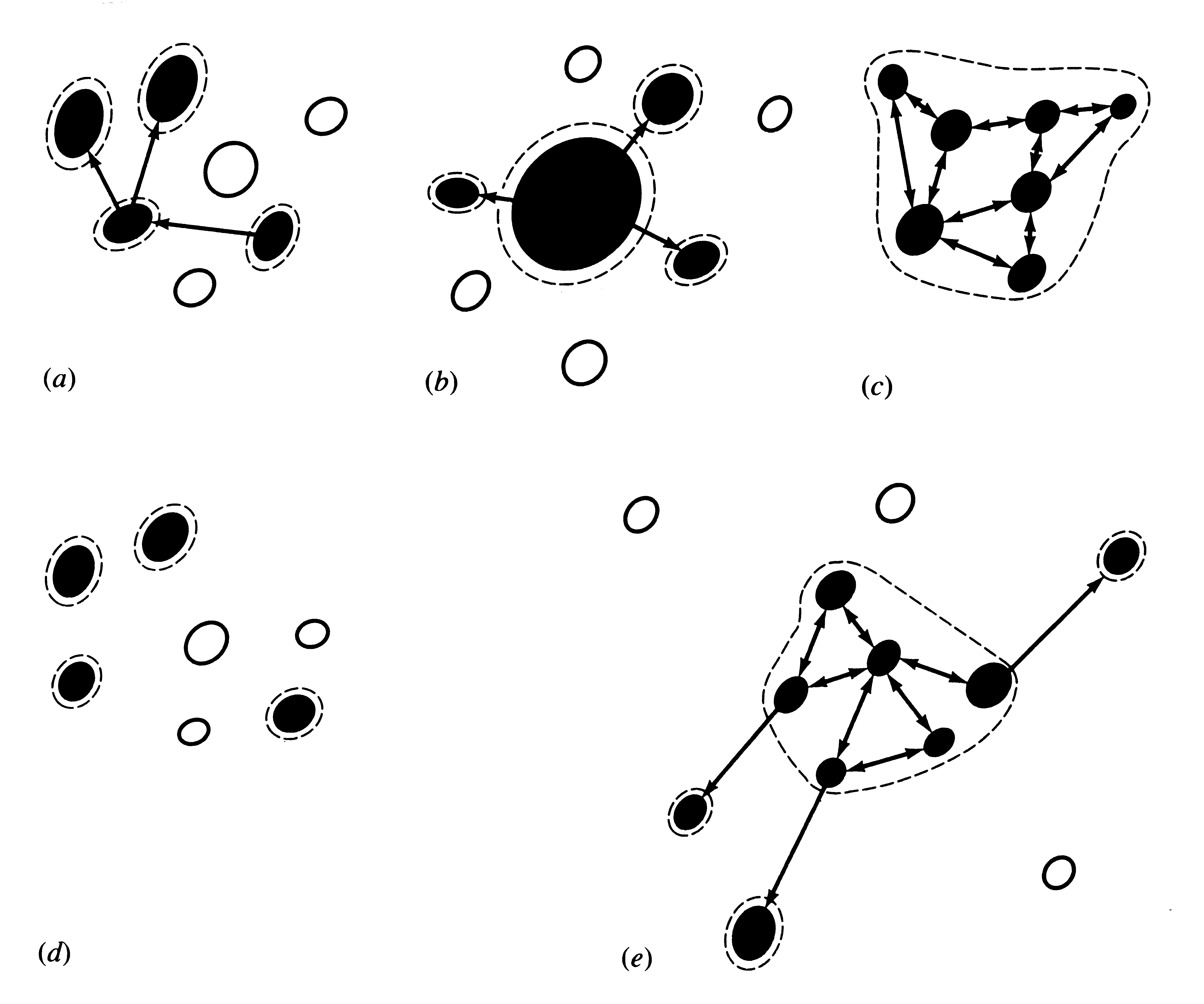
Figure 19.9. Five different kinds of metapopulations. Closed circles represent habitat patches (filled = occupied; unfilled = vacant). Dashed lines indicate boundaries of "populations." Arrows represent migration events (colonizations). (a) Levins's metapopulation. (b) Source-boundary metapopulation. (c) "Patchy" population. (d) Non-equilibrium metapopulation [differs from (a) in that no recolonization occurs]. (e) An intermediate case that combines cases (b) and (c). [Adapted from Harrison (1991).]

More complex models have been developed that relax many of these restrictive simplifying assumptions. For example, Hanski (1982) added a term to the extinction part of the equation that causes the probability of going extinct to fall as the number of patches occupied increases.

dp/dt = mp (1 - p) - ep (1 - p)

This model is neutrally stable, but a stochastic version of it predicts that species fall into two types, regionally common and abundant species that are well-spaced out in niche space ("core" species) and the opposite, rare species that are present only patchily ("satellite" species).

Processes of population turnover, extinction, and re-establishment of new populations constitute the study of metapopulation dynamics. Populations can go extinct within a particular area, but by surviving in an adjacent patch of habitat, still survive in the overall landscape. Animals with active habitat selection such as many species of birds and lizards can reach an ecological and evolutionarily stable equilibrium between source and sink habitats, with periodic dispersal from the former to the latter maintaining the species locally (Pulliam 1988). The evolution of dispersal ability holds central focus in such systems. An appropriate mixture of spatial patchiness coupled with disturbance and dispersal can promote coexistence in competitive systems. The metapopulation concept is closely linked to ideas in landscape ecology, although the much needed bridge between the two new disciplines has not yet been made.

Applied Biogeography: Design of Nature Preserves

Tall grass prairie covered hundreds of thousands of square kilometers in the midwestern United States just a few hundred years ago; today, this natural community has virtually disappeared. No one knows what grasslands in California were like a century ago -- hundreds of species of introduced Mediterranen grasses have largely replaced the original native California grasses. Lowland tropical rain forest is now being destroyed at an alarming rate. Natural communities of all sorts are rapidly being replaced by overgrazed pastures, eroded fields, artificial lakes, golf courses, roads, parking lots, shopping malls, and housing developments. None of the earth's natural communities remain pristine; all have been disturbed either with pesticides and other pollutants or by way of

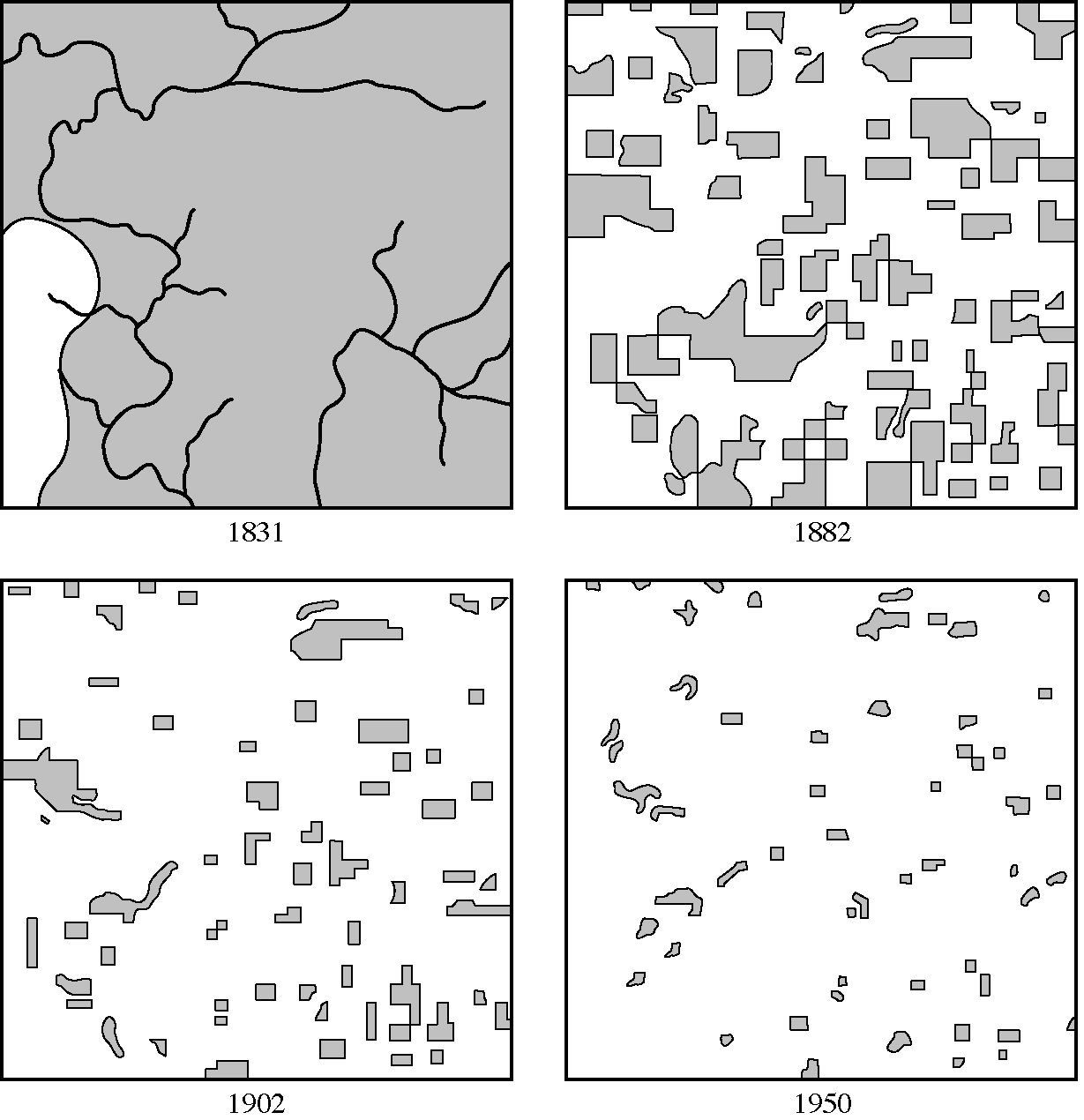
Figure 19.10. Changes in the distribution of forest due to human influence from 1831 to 1950. Imagine what it must look like today! The total area depicted, in Wisconsin, is about 10 km on a side. Fragmentation of the forest has created many very small habitat islands. [From J. T. Curtis, "The Modification of Mid-latitude Grasslands and Forests by Man," in W. L. Thomas, Jr., ed., Man's Role in Changing the Face of the Earth. Copyright © 1956 by The University of Chicago.]

introductions and extinctions of species. Even the disturbed remnants of the earth's biomes are continually being broken up into smaller and smaller isolated patches or habitat islands (Figure 19.10). As would be expected from the equilibrium theory of island biogeography, faunal and floral diversities are decreasing in such isolates as species go extinct locally (some species, such as the passenger pigeon, have been entirely eradicated). Larger species of animals at higher trophic levels disappear before smaller species and those at lower trophic levels. Habitat fragmentation poses a serious threat to many species, including the spotted owl, the golden-cheeked warbler, and the black-capped vireo. Cowbirds have increased greatly in abundance due to human clearing, which has diminished core habitat and increased edge effects. Cowbirds, which are brood parasites on many small songbirds, used to be uncommon, but have increased markedly in abundance due to the increase in amount of edge habitat. Many small songbirds have suffered greatly as a consequence of the resulting increase in brood parasitism. Unfortunately, much remains to be learned about these vanishing natural communities and their inhabitants.

Figure 19.11. Digrammatic representation of the effects of increasing patch size on the relative proportions of edge versus interior habitat. Larger patches support relatively more interior habitat.

Biogeographic principles can be used profitably in designing natural preserves to protect endangered habitats and species. Assume that it is desirable to maintain as great a diversity of plants and animals as possible. Clearly, a single large and contiguous reserve will generally be superior to a number of smaller reserves covering an equivalent area. All else being equal, protected areas should be as diverse as possible. Further, the ratio of edge to area should be minimized. Provision of dispersal corridors or "stepping stones" of natural habitat between larger reserves enhances migration and increases diversity (a species can go extinct in one preserve but re-invade from an adjacent one).

We have now come full circle. In closing, let me remind you of the rapidly disappearing but still unread "book of life" (Rolston 1985): We must move quickly to preserve as much as possible and to read those disappearing pages before they are gone forever.

Selected References

Island Biogeography

Carlquist (1965); Gilbert (1980); MacArthur and Wilson (1963, 1967); Maguire (1963, 1971); Whittaker (1998); Williamson (1981); Wilson (1969); Wilson and Bossert (1971).

Species-Area Relationships

Gleason (1922, 1929); Krebs (1972); MacArthur and Wilson (1967); May (1975a); Odum (1959, 1971); Preston (1948, 1960, 1962a, b); Schoener (1976a).

Equilibrium Theory of Island Biogeography

Brown (1971); Gilbert (1980); MacArthur and Wilson (1963, 1967); Simberloff (1976); Wilson (1969); Wilson and Bossert (1971).

Islands as Ecological Experiments: Some Examples

Carlquist (1965); Greenslade (1968); MacArthur (1972); MacArthur and Wilson (1967); Williamson (1981).

Hawaiian Drosophilidae

Beverley and Wilson (1985); Carson (1973, 1983); Carson and Kaneshiro (1976); Simon (1987); Wagner and Funk (1995); Williamson (1981).

Krakatau

Dammerman (1948); Docters van Leeuwen (1936); MacArthur and Wilson (1967); Whittaker et al. (1989)

The Taxon Cycle

MacArthur and Wilson (1967); Ricklefs and Cox (1972); Wilson (1961).

Experimental Biogeography

Colwell and Winkler (1984); Haydon et al. (1993, 1994).

Conservation Biology

Falk (1992); Fiedler and Jain (1992); Haydon and Pianka (1999); Kareiva, Kingsolver and Huey (1993); Lande (1988); Meffe and Carroll (1994); Menges (1992); Mittermeier et al. (1998); Myers (1988, 1990); Oldfield (1995); Pease and Lande (1995); Pimm (1991); Pimm and Askins (1995); Primack (1998); Simberloff (1992, 1995); Soulé (1986, 1987); Whitmore and Sayer (1992).

Metapopulations

Bengtsson (1989); Boorman and Levitt (1973); Caswell and Cohen (1991); DeAngelis and Waterhouse (1987); Ebenhard (1991); Gilpin and Hanski (1991); Gotelli (1991); Griffis and Jaeger (1998); Hanski (1982, 1998, 1999); Hanski and Gilpin (1991, 1997); Harrison (1991); Harrison et al. (1988); Hassell and May (1990); Hastings (1991); Hastings and Wolin (1989); Haydon and Pianka (1999); Holyoak and Lawler (1996a, 1996b); Karieva 1990; Levins (1969, 1970); Pulliam (1988); Pulliam and Danielson (1991); Sjogren (1991); Verboom et al. (1991).

Applied Biogeography: Design of Nature Preserves

Boecklen and Bell (1987); Dyer (1995); Heinen (1995); Meffe and Carrol (1994); Rolston (1985, 1995); Shafer (1990); Simberloff (1992); Terborgh (1974a, 1974b); Wilson and Willis (1975).