|
Reproductive Tactics Eric R. Pianka Theory Costs of reproduction Tradeoffs between present progeny and expectation of future progeny. Reproductive effort, relative clutch mass (RCM) Residual reproductive value Expenditure per progeny (EPP), neonate size Triumvirate: Clutch size = RCM/EPP Age of onset of sexual maturity, single brood vs. multiple clutches r selection verus K selection (r-K selection continuum) Bet hedging (unpredictable variable juvenile mortality) External versus internal fertilization (certainty of paternity) Parental care Acting through differential reproductive success, natural selection has produced a great diversity of reproductive tactics, each of which presumably must correspond to a local optimum that maximizes an individual's lifetime reproductive success in its particular environment. Such an optimal reproductive tactic maximizes an individual's reproductive value (the sum of all present plus the expected probable number of all future offspring) at every age. Reproductive effort (parental investment in current reproduction) should vary inversely with expectation of future offspring. The precise form of the tradeoff between present progeny and future offspring is itself sensitive to a wide variety of environmental factors, especially resource availability and conditions for survival. A compromise must be reached between producing many small progeny versus fewer large ones: this results in an optimal expenditure per progeny which mazimizes parental fitness (the total fitnesses of all progeny). Optimal clutch size is a necessary consequence of reproductive effort and expenditure per progeny. Selection in crowded environments differs from that in uncrowded environments, the former favoring larger more competitive offspring and the latter early reproduction, high reproductive effort, low expenditure per progeny and large clutch size. Early reproduction is advantageous in expanding (opportunistic) populations, whereas reproduction may be delayed without cost in equilibrium populations. Sexual selection appears to be weak in seasonal breeders, but may be intense in both opportunistic and equilibrium populations. Reproductive tactics can be placed on a two dimensional triangular surface in three space with the coordinates: juvenile survivorship, fecundity, and age of first reproduction (or generation time). Reproductive tactics among fishes (and probably all organisms) fall on this two-dimensional triangular surface with three endpoints corresponding to equilibrium (K-strategists), opportunistic, and seasonal species (Winemiller 1992). The r-K selection continuum runs diagonally across this surface from the equilibrium corner to the opportunistic-seasonal edge, and a bet-hedging axis passes across this triangular surface from the opportunistic corner endpoint to the edge connecting the seasonal and equilibrium tactics. Sexual selection appears to be weak in seasonal breeders, but may be intense in both opportunistic and equilibrium populations. 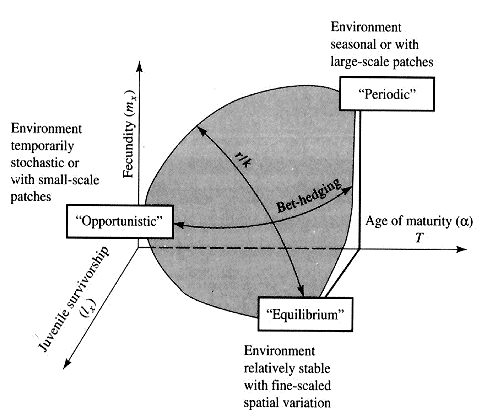
Sexual reproduction remains an evolutionary enigma because organisms practicing it necessarily dilute their genetic contribution to their own offspring by half, requiring that twice as many progeny be produced for the same reproductive success. In contrast, creatures reproducing asexually replicate only their own genes. Evolutionary advantages of sexual reproduction, such as genetic variability and a consequent ability to track a changing environment, must be substantial in order to outweigh the costs of halved heritability. Several possible advantages to individuals (as opposed to populations) include: (1) the possibility of mating with a very fit member of the opposite sex, thereby associating one's own genes statistically with genes conferring high fitness, (2) reduced competition among siblings, and (3) heterozygosity itself might confer enhanced fitness. Squamate reproductive tactics have attracted considerable attention (Ballinger 1983; Tinkle 1969; Tinkle et al 1970; Tinkle and Hadley 1975; Vitt and Congdon 1978; Vitt and Price 1982; Dunham et al. 1988). Most lizards and snakes lay eggs, but some species retain their eggs internally and give birth to living young. Live-bearing has arisen repeatedly among squamates, even multiple times within a single genus: Viviparity has arisen in at least eight different families (agamids, anguids, chameleons, geckos, phrynosomatids, lacertids, skinks, and xantusids). Shine and Bull (1979) conservatively estimate at least 28 independent origins of viviparity [Shine (1985) suggests even more must have occurred]. Live bearing and egg retention is more prevalent in cooler regions at high elevations and high latitudes (Tinkle and Gibbons, 1977; Shine and Bull, 1979). Average clutch size varies from one to fifty or more among different species of lizards and snakes (Fitch 1970). Snakes are more prolific than lizards. Fully grown adult Python reticulatus females are on record with clutches of a hundred eggs (Fitch 1970). Some species reproduce only once every second or third year, others but once each year, while still others lay two or more clutches each year. Lizards that lay only one egg or give birth to a single young include the American iguanid genus Anolis, the Kalahari skink Typhlosaurus gariepensis, and the geckos Gehyra variegata and Ptenopus garrulus. Clutch size is fixed at one or two eggs in certain families (Geckos, Pygopodids) and genera (Anolis). Across species, modal clutch size among lizards is 2, whereas it is about 6-8 among snakes (Fitch 1970). In the Kalahari agamid Agama aculeata, clutch size averages 13. Clutch sizes in certain horned lizards are still larger, averaging 24.3 in the American phrynosomatid Phrynosoma cornutum (the Texas horned lizard). One of the most fecund lizards is Ctenosaura pectinata, one female of which had 49 eggs in her oviducts (Fitch 1970). Clutch or litter sizes vary from one to forty or more among different species of lizards. Some species reproduce only once every second or third year, others but once each year, while still others lay two or more clutches each year. Substantial spatial and temporal variation in clutch size also exists between species. Substantial spatial and temporal variation in clutch size also exists within species. As just one of many possible examples, in the double-clutched Australian agamid species Ctenophorus isolepis (Pianka 1971), the size of 67 first clutches (August-December) averaged 3.01 eggs whereas the mean of 41 second clutches (January-February) was 3.88. Females increase in size during the season, and, as in many lizards, larger females tend to lay larger clutches. Interestingly enough, however, these same females appear to be investing relatively more on their second clutches than they are on their first clutch: among, 25 first clutches, clutch volumes average only 11.2% of female weight, but in 15 second clutches the average is 15.1%. (95% confidence intervals on these means are non-overlapping -- 10.3 to 12.2 versus 13.4 to 16.9, respectively -- Pianka and Parker 1975). Changes in fecundity with fluctuations in food supplies and local conditions from year to year or spot to spot have also frequently been observed: for example, in the North American whiptail Aspidoscelis tigris (Family Teiidae) females lay larger clutches in years with above-average precipitation and presumably ample food supplies (Pianka 1986). Similar phenomena have also been documented in Xantusia vigilis (Zweifel and Lowe 1966) and Uta stansburiana and doubtlessly occur in many or even most other lizard species. Clutch or litter weight (or volume), expressed as a fraction of a female's total body weight, ranges from as little as 4 to 5% in some species to as much as 20-30% in others. Clutch weights tend to be particularly high in some of the North American horned lizards (genus Phrynosoma). Ratios of clutch or litter weight to female body weight, also known as relative clutch mass (RCM), correlate strongly with various energetic measures and have often been used as crude indices of a female's instantaneous investment in current reproduction (sometimes equated with the elusive notion of "reproductive effort"). Expenditure per Progeny Even if we neglect the genetic component, not all offspring are equivalent. Progeny produced late in a growing season often have lower probabilities of reaching adulthood than those produced earlier -- hence, they contribute less to enhancing parental fitness. Likewise, larger offspring may usually cost more to produce, but they are also "worth more." How much should a parent devote to any single progeny? For a fixed amount of reproductive effort, average fitness of individual progeny varies inversely with the total number produced. One extreme would be to invest everything in a single very large but extremely fit progeny. Another extreme would be to maximize the total number of offspring produced by devoting a minimal possible amount to each. Parental fitness is often maximized by producing an intermediate number of offspring of intermediate fitness: Here, the best reproductive tactic is a compromise between conflicting demands for production of the largest possible total number of progeny and production of offspring of the highest possible individual fitness (see also section on r and K selection). 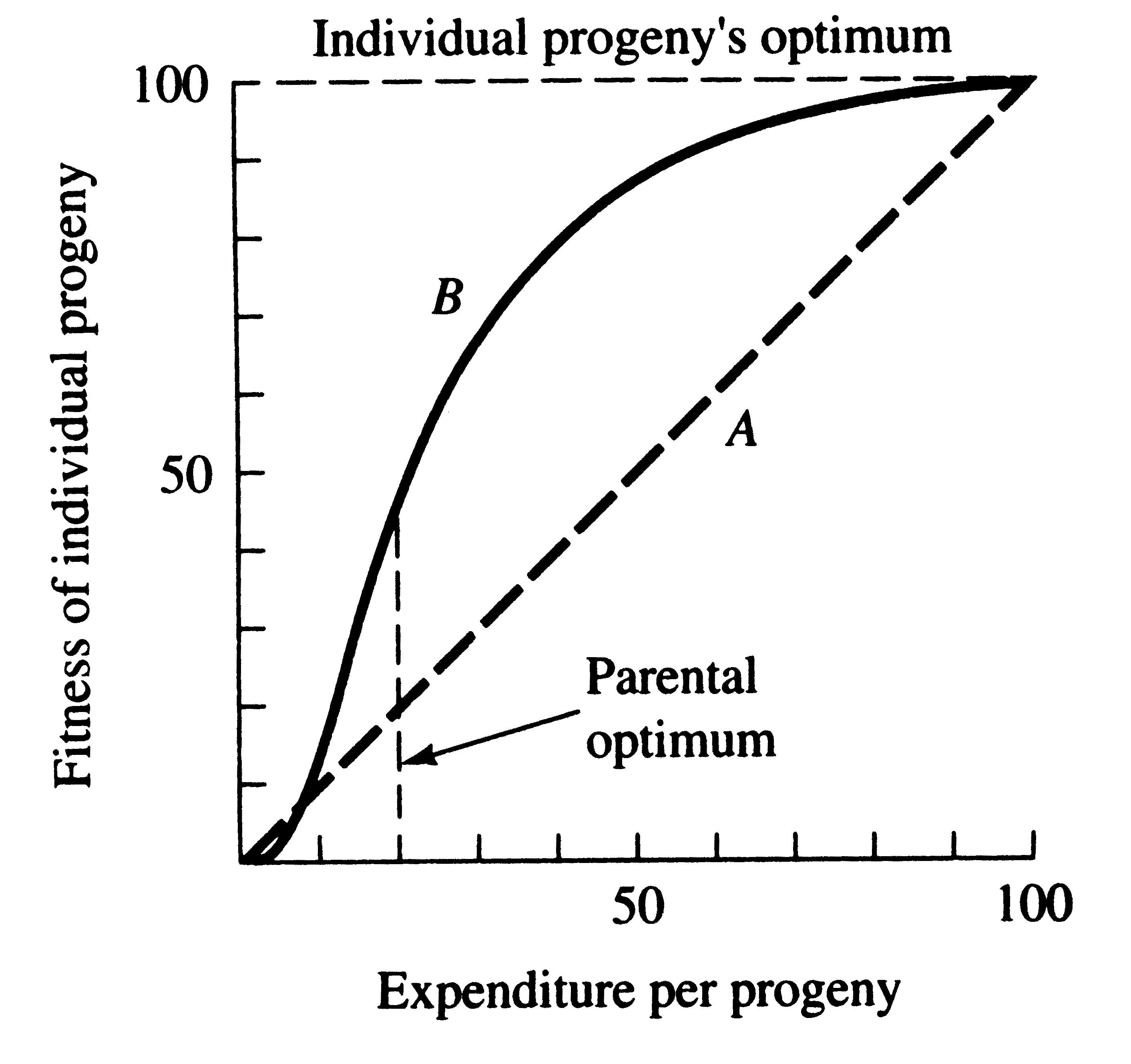
A simple graphical model illustrates this fundamental tradeoff between quantity and quality of offspring (Figures). In the unlikely event that progeny fitness increases linearly with parental expenditure (dashed line A in left Figure), fitness of individual progeny decreases with increased clutch or litter size (the lowermost dashed curve A in right Figure). However, because parental fitness (the total of the fitnesses of all progeny produced) is flat, no optimal clutch size exists from a parental viewpoint (upper dashed line A in right Figure). Gains in progeny fitness per unit of parental investment are likely to be greater at lower expenditures per progeny than at higher ones because the proportional increase per unit of allocation is greater at low levels of investment; curves level off at higher expenditures due to the law of diminishing returns. If the biologically plausible assumption is made that progeny fitness increases sigmoidally with parental investment (curve B in left Figure), there is an optimal parental clutch size (peak of uppermost curve B in right Figure). In this hypothetical example, parents that allocate only 20 percent of their reproductive effort to each of five offspring gain a higher total return on their investment than parents opting for any other clutch size (right Figure). Such curves have been demonstrated for starlings and swifts (Lack 1954) Although such a tactic is optimal for parents, it is not the optimum for individual offspring, which would achieve maximal fitness when parents invest everything in a single offspring. Hence, a "parent-offspring conflict" exists (Trivers 1974). The exact shape of the curve relating progeny fitness to parental expenditure in any real organism is influenced by a virtual plethora of environmental variables, including length of life, body size, survivorship of adults and juveniles, population density, and spatial and temporal patterns of resource availability. The competitive environment of immatures is likely to be of particular importance because larger, better-endowed offspring should usually enjoy higher survivorship and generally be better competitors than smaller ones. In addition to clutch size and female total investment in reproduction, the size (or weight) of an individual oviductal egg or newborn progeny, also varies widely among lizards from as little as 1-2% in some species to a full 17% in the live-bearing Kalahari fossorial skink Typhlosaurus gariepensis. Such expenditures per progeny are inverse measures of the extent to which a juvenile lizard must grow to reach adulthood. Clutch or Litter Size Juveniles and adults are often subjected to very different selective pressures. Reproductive effort should reflect environmental factors operating upon adults, whereas expenditure per progeny will be strongly influenced by juvenile environments. Because any two parties of the triumvirate determine the third, an optimal clutch or litter size is a direct consequence of an optimum current reproductive effort coupled with an optimal expenditure per progeny (indeed, clutch size is equal to reproductive effort divided by expenditure per progeny). Of course, clutch size can be directly affected by natural selection as well. For example, it has been suggested that all members of the lizard genus Anolis lay but a single egg because the ancestral stock was arboreal and encountered intense selection against being weighted down by a heavy egg load, becoming genetically fixed at a clutch size of one (Andrews and Rand 1974). Any two parties to this triad (clutch size, female reproductive investment, and expenditure per progeny) uniquely determine the third: however, forces of natural selection molding each differ substantially. Thus clutch or litter weight presumably reflects an adult female's best current investment tactic in a given environment at a particular instant in time whereas expenditure on any given individual progeny is probably more closely attuned to the average environment to be encountered by a juvenile. In a sense, then, clutch (or litter) size is the direct result of the interaction between an optimal parental reproductive tactic and an optimal juvenile body size (clutch size is simply the ratio of the former divided by the latter). Statistics on clutch/litter sizes, total reproductive investment of females, and expenditure per progeny among 65 species of desert lizards were presented by Pianka (1986), along with similar data on another 20 species of lizards, including both desert and non-desert forms extracted from the literature. Among the species surveyed, average clutch/litter size varies from 1 in the Kalahari skink Typhlosaurus gariepensis and the geckos Gehyra variegata and Ptenopus garrulus to 13 in the Kalahari agamid Agama aculeata. Clutch sizes in certain horned lizards are still larger, averaging 24.3 in the American iguanid Phrynosoma cornutum (the Texas horned lizard). Clutch or litter size and female investment are significantly positively correlated (r = .482, P < .001), although scatter is considerable. Viviparous species (mostly skinks) tend to have slightly higher investment ratios than do the egg layers. Since expenditure per progeny can be estimated from total investment divided by clutch/litter size, it tends to decrease exponentially with increasing number of progeny (for a fixed total investment). Expenditure per progeny and clutch/litter size are inversely related (r = -.652 P < .001). This correlation is strengthened when both variables are transformed to logarithms (on a log-log plot, the correlation coefficient is -.810). Clutch size is thus correlated positively with total investment but negatively with investment per progeny. In simple product-moment correlation, the latter two members of the triumvirate, total reproductive investment and expenditure per progeny, are only weakly and not significantly correlated (r = .153, P < .10), suggesting that these two parameters vary independently of one another and that they may be responsive to different selective pressures. However, when effects of clutch size are held constant by partial correlation, the weak correlation between reproductive effort and expenditure per progeny is substantially improved (partial correlation coefficient = .704), an indication, once again, that these three aspects of reproductive tactics are far from independent of one another. Indeed, pairwise partial correlation coefficients between the logarithms of these three variates are all nearly perfect (r xy.z's = .910, .924, and -.969). Species fall neatly on a plane in this three space, as evidenced by a principal component analysis using log-transformed variables, which shows that the first two principal components reduce variance by over 99% (Pianka 1986). Frequency distributions of average clutch/litter sizes, total investment ratios, and expenditure per progeny among species were summarized by Pianka (1986). Expenditure per progeny varies over more than an order of magnitude, from 1% to 17% of a gravid female's body weight. Interestingly, species with narrow diets often though not always tend to have higher than average expenditures per progeny. Two of the species with the highest expenditures per progeny, Typhlosaurus gariepensis and T. lineatus, probably experience intense competition: (1) these live-bearing, subterranean skinks exist at very high population densities, (2) individuals are long-lived with delayed maturity, (3) litter sizes are extremely small (means of 1.0 and 1.5, respectively), and (4) females very likely reproduce only biennially (Huey et al. 1974). These two Kalahari fossorial skinks are also extreme food specialists, eating termites to the virtual exclusion of all other prey. The extremely high expenditure per progeny of Typhlosaurus may well be necessary to confer newborn animals with competitive ability sufficient to establish themselves in the highly competitive underground environment. Limited evidence indicates that investment per progeny is indeed responsive to and indicative of a lizard's competitive environment. Thus, in Typhlosaurus lineatus, offspring are significantly heavier (and expenditure per progeny significantly greater) where this species occurs in sympatry with T. gariepensis as compared with allopatric populations (Huey et al. 1974). Other food-specialized species seem also to encounter intense competition: among Australian geckos, species with relatively restricted termite diets tend to lay comparatively larger eggs and hence have higher expenditures per progeny than do those with more catholic diets (Pianka and Pianka 1976). A similar phenomenon appears to occur in the semi-arboreal African skink Trachylepis spilogaster: on one study area, it is syntopic with an ecologically very similar species, Trachylepis striata. Expenditure per progeny in T. spilogaster increases significantly (t-test, P < .01) from allopatry (mean = 4.39 + 0.21, N = 51) to sympatry (mean = 5.63 + 0.48, N = 19). Differences between viviparous and oviparous species are relatively slight, although, as noted above, viviparous species appear to invest slightly more in reproduction. Statistically significant differences exist between diurnal and nocturnal species of lizards in these reproductive statistics: nocturnal species have significantly smaller clutch/litter sizes and lower total investment in reproduction, but significantly higher expenditure per progeny (Pianka 1986). These differences between diurnal and nocturnal species stem largely from a simple historical or taxonomic basis, since geckos and pygopodids dominate the nocturnal saurofauna and have a fixed clutch of only one or two eggs. Two viviparous nocturnal skink species (genus Liopholis) also tend to have small litters; however, a third oviparous nocturnal skink, Eremiascincus richardsoni, does not have a small clutch size. Reproductive tactics can be mapped, to a limited extent, on to the spatial-temporal thermoregulation axis (Pianka 1986). Simple pair-wise product-moment correlation coefficients between the three reproductive variables and the slope-intercepts of body temperature regressions on air temperature are weak although generally statistically significant. The strongest correlation, between the logarithm of clutch size and the intercept of body temperature on air temperature (r = .609), seems to arise largely as a result of the small clutch sizes and low body temperature intercepts of nocturnal lizards. r and K selection A concept that has proven to be quite useful on which to hang numerous aspects of reproductive tactics is known as r and K selection. Periodic disturbances, including fires, floods, hurricanes, and droughts, often result in catastrophic density-independent mortality, suddenly reducing population densities well below the maximal sustainable level for a particular habitat. Populations of annual plants and insects typically grow rapidly during spring and summer but are greatly reduced at the onset of cold weather. Because populations subjected to such forces grow in erratic or regular bursts, they have been termed opportunistic populations. In contrast, populations such as those of many vertebrates may usually be closer to an equilibrium with their resources and generally exist at much more stable densities (provided that their resources do not fluctuate); such populations deplete their resources and are called equilibrium populations. Clearly, these two sorts of populations represent end points of a continuum; however, the dichotomy is useful in comparing different populations. The significance of opportunistic versus equilibrium populations is that density-independent and density-dependent factors and events differ in their effects on natural selection and on populations. In highly variable and/or unpredictable environments, catastrophic mass mortality presumably often has relatively little to do with the genotypes and phenotypes of the organisms concerned or with the size of their populations. (Some degree of selective death and stabilizing selection has been demonstrated in winter kills of certain bird flocks.) By way of contrast, under more stable and/or predictable environmental regimes, population densities fluctuate less and much mortality is more directed, favoring individuals that are better able to cope with high densities and strong competition. Organisms in highly rarefied environments seldom deplete their resources to levels as low as do organisms living under less rarefied situations; as a result, the former usually do not encounter such intense competition. In a "competitive vacuum" (or an extensively rarefied environment) the best reproductive strategy is often to put maximal amounts of matter and energy into reproduction and to produce as many total progeny as possible (even small ones) as soon as possible. Because there is little competition, these offspring often can thrive even if they are quite small and therefore energetically inexpensive to produce. There is a premium on early reproduction, because progeny produced sooner can themselves reproduce earlier. (The analogy of interest accruing in a bank account is apt.) However, in a "saturated" environment, where density effects are pronounced and competition is keen, the best strategy may often be to put more energy into competition and maintenance and to produce offspring with more substantial competitive abilities. This usually requires larger offspring, and because they are energetically more expensive, it means that fewer can be produced. Reproduction is less urgent in such a crowded situation and reproduction may be postponed until opportunities are particularly good. A baby produced later is worth as much as one produced earlier (unlike the situation in expanding populations). These two opposing selective forces were designated r selection and K selection by MacArthur and Wilson (1967), after the two terms in the logistic equation. One should not take these terms too literally, however, as the concepts are independent of the equation. They are also known as density-independent and density-dependent selection. Of course, things are seldom so black and white, but there are usually all shades of gray. No organism is completely r selected or completely K selected; rather all must reach some compromise between these two extremes. Indeed, one can think of a given organism as an "r-strategist" or a "K-strategist" only relative to some other organism; thus statements about r and K selection are invariably comparative. Cats and dogs are r-selected compared to humans, but K-selected compared to mice and rats. Mice and rats, in turn, are K-selected compared to most insects. We can think of an r-K selection continuum and an organism's position along it in a particular environment at a given instant in time (Pianka 1970). A variety of correlates of these two kinds of selection are listed in Table 1. Parental care and live bearing (viviparity) constitute a means of increasing expenditure per progeny, and are often a response to crowding and consequent competition as well. In squamate reptiles (lizards and snakes), viviparity has arisen at least 100 times and is associated with cool climates. An interesting special case of an opportunistic species is the fugitive species, envisioned as a predictably inferior competitor always being excluded locally by interspecific competition but which manages to persist in newly disturbed regions by virtue of high fecundity and dispersal ability (Hutchinson 1951). Such a colonizing species can persist in a continually changing patchy environment in spite of pressures from competitively superior species. Hutchinson (1961) used another argument to explain the apparent "paradox of the plankton," the coexistence of many species in diverse planktonic communities under relatively homogeneous physical conditions, with limited possibilities for ecological separation. He suggested that temporally changing environments may promote diversity by periodically altering relative competitive abilities of component species, thereby allowing their coexistence. Recently, McClain (1991) suggested that the relative strength of sexual selection depends on the life history strategy, with r-strategists being less likely to be subjected to strong sexual selection than K-strategists. Winemiller (1989, 1992) points out that reproductive tactics among fishes (and probably all organisms) can be placed on a two dimensional triangular surface in three space with the coordinates: juvenile survivorship, fecundity, and age of first reproduction (or generation time). This two-dimensional triangular surface has three vertices corresponding to equilibrium (K-strategists), opportunistic, and seasonal species. The r-K selection continuum runs diagonally across this surface from the equilibrium corner to the opportunistic-seasonal edge. In fish, seasonal breeders exhibit little sexual dimorphism, whereas both opportunistic and equilibrium species display marked sexual dimorphisms (Winemiller 1992). 
Multivariate Analyses of Squamate Reproduction Dunham and Miles (1985) undertook a detailed multivariate analysis of the reproductive tactics of 91 species of lizards. A discriminant function analysis describes an axis which has actively foraging species with large body sizes and small clutches at one end and sit-and-wait foragers with small body size and large clutches at the other end. Another multivariate statistical analysis identified three clusters of life historical patterns among both snakes and lizards (Dunham et al. 1988): (1) single brooded, oviparous species, (2) multiple brooded, oviparous species, and (3) single brooded, viviparous species. In addition, a fourth pattern emerged for a few lizards and snakes: (4) biennial, viviparous. Recently, Bauwens and Diaz-Uriarte (1997) described a unidimensional continuum for a clade of lacertid lizards after removing the effects of phylogeny via independent contrasts: early maturing, short-lived, small sized, small clutch sized, large progeny, multiple brooded species were at one end of the spectrum and large, long-lived, delayed maturity, single clutched, large clutch size, small progeny were at the other. Such axes could be exploited as dimensions for construction of "periodic tables of lizard niches" (Pianka 1993). References on Reproductive Tactics Ballinger, R. E. 1983. Life-History Variations. Chapter 11 (pp. 241-260) in Lizard Ecology: Studies of a Model Organism, edited by R. B. Huey, E. R. Pianka, and T. W. Schoener. Harvard University Press. Bauwens, D. and R. Diaz-Uriarte. 1997. Covariation of life history traits in lacertid lizards: a comparative study. Amer. Natur. 149: 91-111. Brockelman, W. Y. 1975. Competition, the fitness of offspring, and optimal clutch size. Amer. Natur. 109: 677-699. Cole, L. C. 1954. The population consequences of life history phenomena. Quart. Rev. Biol. 29: 103-137. Crews, D. 1984. Gamete preduction, sex hormone secretion, and mating behavior uncoupled. Hormones and Behavior 18: 22-28. Crump, M. L. 1974. Reproductive strategies in a tropical anuran community. Misc. Publ. Mus. Nat. Hist. Univ. Kansas 61: 1-68. Duellman, W. E. and L. Treub. 1986. Biology of amphibians. McGraw-Hill, New York. Dunham, A. E. and D. B. Miles. 1985. Patterns of covariation in life history traits of squamate reptiles: the effects of size and phylogeny reconsidered. American Naturalist 126: 231-257. Dunham, A. E., D. B. Miles, and D.N. Reznick. 1988. Life history patterns in squamate reptiles. Chapter 7 (pp. 441-522) in C. Gans and R.B. Huey (eds.) Biology of the Reptilia, Volume 16, Ecology B. Defense and Life History. Alan R. Liss, Inc., New York. Emlen, J. M. 1970. Age specificity and ecological theory. Ecology 51: 588-601. Fitch, H. S. 1970. Reproductive cycles in lizards and snakes. Misc. Publ. Univ. Kansas Mus. Nat. Hist. 52: 1_-247. Gadgil, M. and W. H. Bossert. 1970. Life historical consequences of natural selection. Amer. Natur. 104: 1-24. Gadgil, M., and O. T. Solbrig. 1972. The concept of r and K selection: Evidence from wild flowers and some theoretical considerations. Amer. Natur. 106: 14-31. Goodman, D. 1974. Natural selection and a cost ceiling on reproductive effort. Amer. Natur. 108: 247-268. Grime, J. P. 1977. Evidence for the existence of three primary strategies in plants and its relevance to ecological and evolutionary theory. Amer. Natur. 111:1169-1194. Grime, J. P. 1979. Plant strategies and vegetation processes. Wiley, New York. Howard, R. D. 1988. Reproductive success in two species of anurans. Chapter 7 (pp. 99-113) in Clutton-Brock, T. H. (ed.) Reproductive Success. Univ. Chicago Press. Huey 1977. Egg retention in some high altitude Anolis lizards. Copeia 1977: 373-375. Huey, R. B., E. R. Pianka, M. E. Egan, and L. W. Coons. 1974. Ecological shifts in sympatry: Kalahari fossorial lizards (Typhlosaurus). Ecology 55:304-316. Hutchinson, G. E. 1951. Copepodology for the ornithologist. Ecology 58: 571-577. Hutchinson, G. E. 1961. The paradox of the plankton. Amer. Natur. 95: 137-145. MacArthur, R. H. and E. O. Wilson. 1967. The theory of island biogeography. Princeton Univ. Press. McLain, D. K. 1991. The r-K continuum and the relative effectiveness of sexual selection. Oikos 60: 263-265. Murphy, G. I. 1968. Pattern in life history and environment. Amer. Natur. 102: 390-404. Niewiarowski, P H. 1994. Understanding geographic life-history variation in lizards. Chapter 2 (pp. 31-49) in L. J. Vitt and E. R. Pianka (eds.) Lizard Ecology: Historical and Experimental Perspectives. Princeton Univ. Press. Pianka, E.R. 1969. Notes on the biology of Varanus caudolineatus and Varanus gilleni. Western Australian Naturalist 11: 76-82. Pianka, E.R. 1970. Comparative autecology of the lizard Aspidoscelis tigris in different parts of its geographic range. Ecology 51: 703-720. Pianka, E. R. 1971. Ecology of the agamid lizard Amphibolurus isolepis in Western Australia. Copeia 1971: 527-536. Pianka, E. R. 1976. Natural selection of optimal reproductive tactics. American Zoologist 16: 775-784. Pianka, E. R. 1986. Ecology and Natural History of Desert Lizards. Analyses of the Ecological Niche and Community Structure. Princeton University Press, Princeton, New Jersey. Pianka, E. R. 1992. Reproductive tactics. Pages 189-209 in R. Dallai (ed.) Sex origin and evolution. Proc. of International Symposium on Origin and Evolution of Sex, Siena, September 9-11, 1991. Mucchi Editore, Italy. Pianka, E. R. 1993. The many dimensions of a lizard's ecological niche. Chapter 9 (pp. 121-154) in E. D. Valakos, W. Bohme, V. Perez-Mellado, and P. Maragou (eds.) Lacertids of the Mediterranean Basin. Hellenic Zoological Society. University of Athens, Greece. Pianka, E. R. and W. S. Parker. 1975. Age-specific reproductive tactics. American Naturalist 109: 453-464. Pianka, E. R. and H. D. Pianka. 1976. Comparative ecology of twelve species of nocturnal lizards (Gekkonidae) in the Western Australian desert. Copeia 1976: 125-142. Rand, A. S. 1967. Predator-prey interactions and the evolution of aspect diversity. Atas do Simposio sobre a Biota Amazonica 5: 73-83. Schall, J. J. and E. R. Pianka. 1980. Evolution of escape behavior diversity. Amer. Natur. 115: 551-566. Schoener, T. W. 1979. Inferring the properties of predation and other injury-producing agaents from injury frequencies. Ecology 60: 1110-1115. Schwarzkopf, L. 1994. Measuring trade-offs: a review of studies of costs of reproduction in lizards. Chapter 1 (pp. 7-29) in L. J. Vitt and E. R. Pianka (eds.) Lizard Ecology: Historical and Experimental Perspectives. Princeton Univ. Press. Shine, R. 1980. Costs of reproduction in reptiles. Oecologia 46: 92-100. Shine, R. and J. J. Bull. 1979. The evolution of live bearing in lizards and snakes. Amer. Natur. 113: 905-923. Shine, R. and L. Schwarzkopf. 1992. The evolution of reproductive effort in lizards and snakes. Evolution 46: 62-75. Sinervo, B. 1994. Experimental tests of reproductive allocation paradigms. Chapter 4 (pp. 73-90) in L. J. Vitt and E. R. Pianka (eds.) Lizard Ecology: Historical and Experimental Perspectives. Princeton Univ. Press. Stearns, S. C. 1976. Life history tactics: a review of the ideas. Quart. Rev. Biol. 51: 3-47. Vitt, L. J., J. D. Congdon, and N. Dickson. 1977. Adaptive strategies and energetics of tail autotomy in lizards. Ecology 58: 326-337. Wilbur, H. M. and P. J. Morin. 1988. Life history evolution in turtles. Chapter 6 (pp. 387-439) in C. Gans and R.B. Huey (eds.) Biology of the Reptilia, Volume 16, Ecology B. Defense and Life History. Alan R. Liss, Inc. Winemiller, K. O. 1992. Life history strategies and the effectiveness of sexual selection. Oikos 63:318-327. Zweifel, R. G. and C. H. Lowe. 1966. The ecology of a population of Xantusia vigilis, the desert night lizard. American Museum Novitates 2247: 1-57. |