|
| |
|
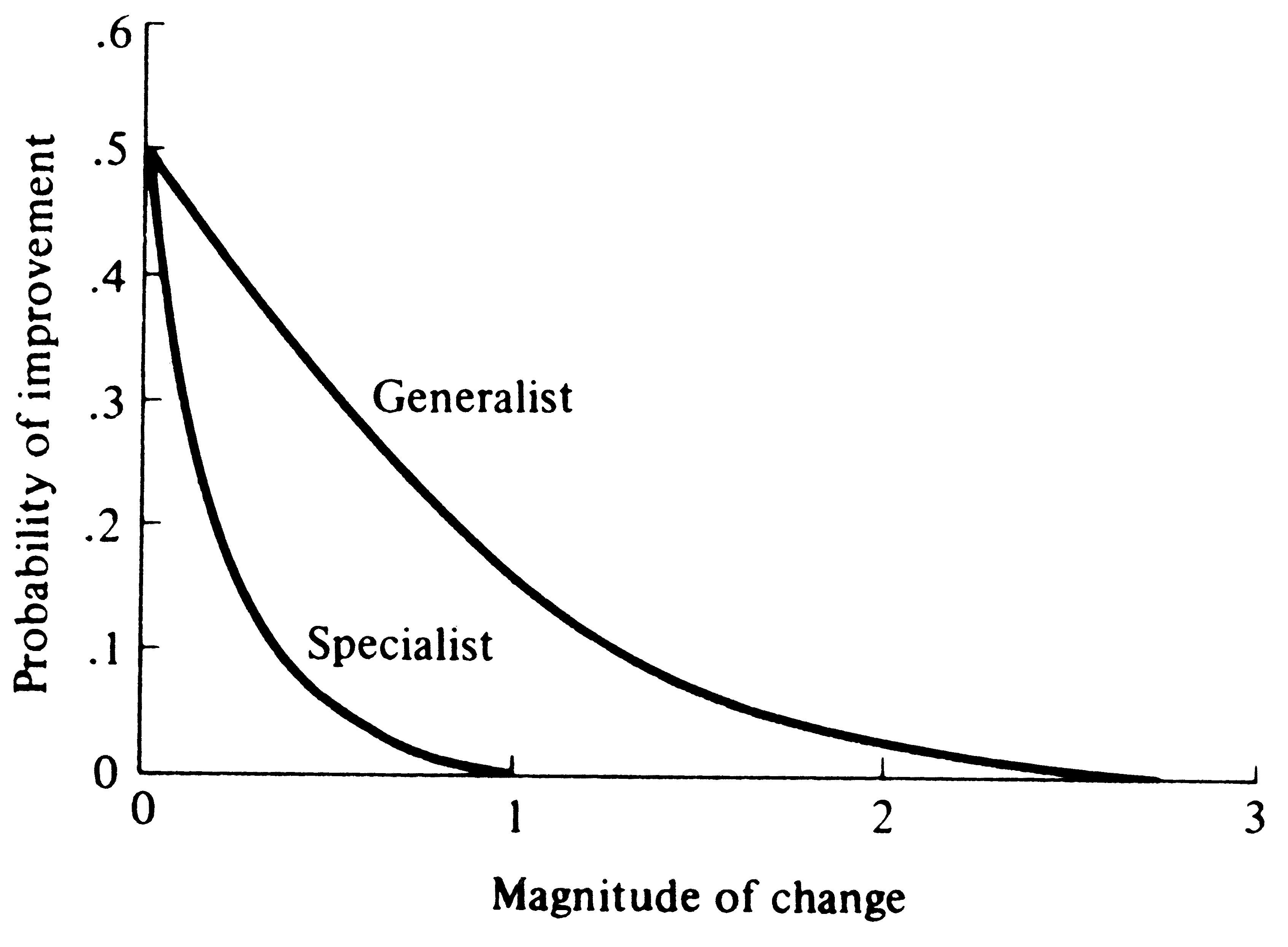
© Eric R. Pianka Adaptation and Deterioration of Environment A simple but elegant model of adaptation and undirected environmental deterioration was developed by Fisher (1930). He reasoned that no organism is "perfectly adapted" -- all must fail to conform to their environments in some ways and to differing degrees. However, a hypothetical, perfectly adapted organism can always be imagined (actually this reflects the environment) against which existing organisms may be compared. Fisher's mathematical argument is phrased in terms of an infinite number of "dimensions" for adaptation (only three are used here for ease of illustration). Imagine an adaptational space of three coordinates representing, respectively, the competitive, predatory, and physical environments (Figure 1). An ideal "perfectly adapted" organism lies at a particular point (say A) in this space, but any given real organism is at another point (say B), some distance, d, away from the point of perfect adaptation. Changes in the position of A correspond to environmental changes making the optimally adapted organism different; changes in B represent changes in the organisms concerned, such as mutations. The distance between the two points, d, represents the degree of conformity between the organism and environment, or the level of adaptation. Fisher noted that very small undirected changes in either organism or environment have a 50:50 chance of being to the organism's advantage (i.e., reducing the distance between A and B). The probability of such improvement is inversely related to the magnitude of the change (Figure 2). 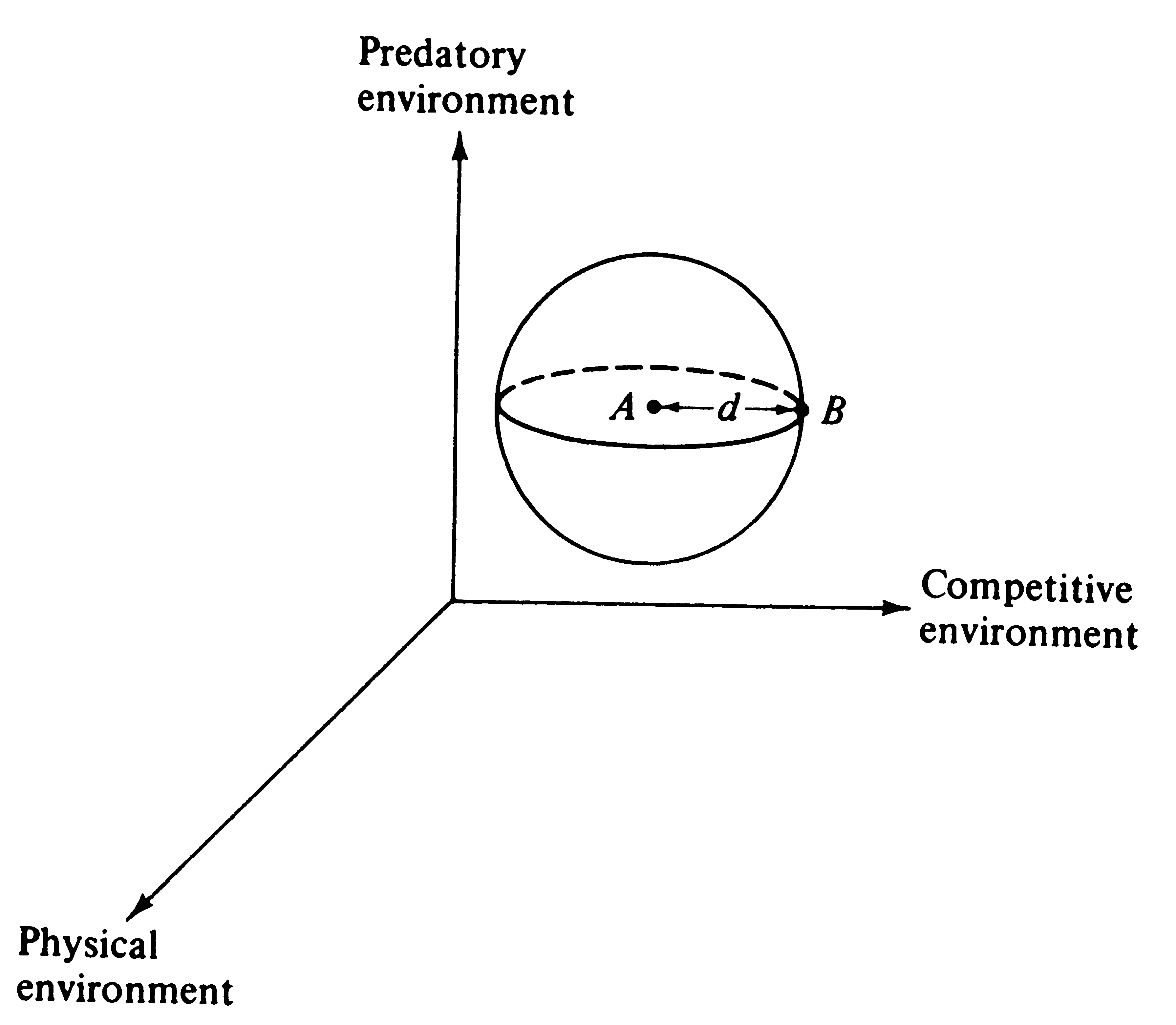
|
|
|
Very great changes in either organism or environment are always maladaptive because even if they are in the correct direction, they "overshoot" points of closer adaptation. (Of course, it is remotely possible that such major environmental changes or "macromutations" could put an organism into a completely new adaptive realm and thereby improve its overall level of adaptation.) Fisher makes an analogy with focusing a microscope. Very fine changes are as likely as not to improve the focus, but gross changes will almost invariably throw the machine further out of focus. Organisms may be thought of as "tracking" their environments in both ecological and evolutionary time, changing as their environments change; thus, as point A shifts because of daily, seasonal, and long-term environmental fluctuations, point B follows it. Such environmental tracking may be physiological (as in acclimation), behavioral (including learning), and/or genetic (evolutionary), depending on the time scale of environmental change. Reciprocal counterevolutionary responses to other species (prey, competitors, parasites, and predators) constitute examples of such evolutionary tracking, and have been termed coevolution. Individual organisms with narrow tolerance limits, such as highly adapted specialists, generally suffer greater losses in fitness due to a unit of environmental deterioration than generalized organisms with more versatile requirements, all else being equal. Thus, more specialized organisms and/or those with restricted homeostatic abilities cannot tolerate as much environmental change as generalists or organisms with better developed homeostasis (Figure 2). Fisher's model applies only to nondirected changes in either party of the adaptational complex -- such as mutations and perhaps certain climatic fluctuations, or other random events. However, many environmental changes are probably nonrandom. Changes in other associated organisms, especially predators and prey, are invariably antagonistic directed so as to reduce an organism's degree of conformity to its environment; thus, they constitute a deterioration of that organism's environment. Directed changes in competitors can either increase or decrease an organism's level of adaptation, depending on whether they involve avoidance of competition or improvements in competitive ability per se. Directed changes in mutualistic systems would usually tend to improve the overall level of adaptation of both parties. Recently, Frank (2009, 2012) has developed mathematical models relating Fisher's model of evolutionary change to information content. In essence, over evolutionary time natural selection causes populations to accumulate information about their environments. Fisher, Ronald A. 1930. The Genetical Theory of Natural Selection. Clarendon Press, Oxford. Frank, S.A., 2009. Natural selection maximizes Fisher information. Journal of Evolutionary Biology 22: 231-244. Frank, S.A., 2012. Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. Journal of Evolutionary Biology 25: 2377-2396. Pianka, Eric R. 2000. Evolutionary Ecology, 6th ed. Addison-Wesley-Longman, San Francisco. Last updated 18 May 2017 by Eric R. Pianka |